Sat, 15 Dec 2018 14:32:02 GMT
And again, I gave a talk for the best mathematics club of the multiverse, for "younger" students, meaning that this text is not scientific. This is the script for the talk.
We want to prove the following theorem:
Theorem: There is an algorithm of which, with standard set theory, we cannot decide whether it terminates.
Firstly, we need to look at what an algorithm is. Usually, people introduce this with Turing machines. However, we will use a model which is closer to modern computers, so-called register machines. These are provably equivalent to Turing machines, except that some algorithms might take a bit longer on Turing machines – but at this point, we do not care about efficiency, we just care about whether things can be calculated at all, given enough time and space. If you care about efficiency, that would be in the realm of complexity theory, while we will work in the realm of recursion theory.
A register machine has a finite set of registers R[0], R[1], …,
which can contain arbitrarily large natural numbers. A program
consists of a sequence of instructions:
- For every i, there is the instruction
R[i]++, which increases the number that is contained inR[i]. - For every i, there is the instruction
R[i]--, which decreases the number contained inR[i]if it is larger than 0, and does nothing otherwise. - There is the instruction
End, which ends the program. - For every i and n, there is the instruction
if R[i]==0 then goto n. The instructions are numbered, and this instruction jumps to the instruction with numbern, ifR[i]contains 0, otherwise it does nothing.
The following program checks whether R[0] >= R[1], and if so, it
sets R[2] to 1:
0 if R[1]==0 then goto 6
1 if R[0]==0 then goto 5
2 R[1]--
3 R[0]--
4 if R[2]==0 then goto 0
5 End
6 R[2]++
7 End
Line 4 is only here to do an unconditional jump, therefore, we can introduce a shorthand that just does an unconditional jump:
0 if R[1]==0 then goto 6
1 if R[0]==0 then goto 5
2 R[1]--
3 R[0]--
4 goto 0
5 End
6 R[2]++
7 End
To make it a bit more readable, we can omit the line numbers, which we usually do not need, and just set labels to the lines we want to jump to:
Start: if R[1]==0 then goto Yes
if R[0]==0 then goto No
R[1]--
R[0]--
goto Start
No: End
Yes: R[2]++
End
This just increases readability, it doesn't make anything possible
that wasn't possible before. By using this algorithm, we can generally
check whether R[i] > R[j], and therefore, we can introduce a
shorthand notation if R[i] > R[j] then goto A without being able to
do anything we couldn't do before.
We can do addition by
Start: if R[1]==0 then goto Done
R[0]++
R[1]--
goto Start
Done: End
and truncated subtraction () by
Start: if R[1]==0 then goto Done
R[0]--
R[1]--
goto Start
Done: End
Therefore, we can add the instructions R[i]+=R[j] which adds R[j]
to R[i], and R[i]-=R[j], without being able to do anything more
than before. Having these instructions, we can define multiplication
by repeated addition, and division and modulo by repeated
subtraction. This is left to the reader.
Now, we cannot know for sure whether everything that is computable at all is computable by register machines. However, we do not know any computable function that cannot be computed by a register machine. Hence, it is generally believed that there is none. This is called the Church-Turing thesis.
These programs operate on numbers only. Real computers work with
images and text. However, this is, computationally, no difference, and
there are several injections between these kinds of data. Especially,
programs themselves can be represented as numbers, which is called
Gödelization. For this, we use the Cantor Pairing, which
gives a bijective function
by
. This function
enumerates the backward diagonals on the grid of natural numbers, as
this graphic shows. The pairing itself can obviously be
calculated with the above functions by a register machine. Inverting
the function is also easy, and left to the reader.
Now we can represent every program we have in the following way: We first map numbers to the single instructions:
R[i]++is mapped toR[i]--is mapped toif R[i]==0 then goto jis mapped toEndis mapped to
Therefore, every instruction has its own code. A program can be
encoded as a sequence of these codes; the program with the
instructions can be encoded by
.
Therefore, it is well-defined to talk about "programs getting other programs as parameters". And having seen this, it is easy to write an universal register machine, which evaluates such a program, given a sequence of register values:
The state of a program is entirely determined by its registers and the
number of the current instruction. It has a finite sequence of
registers , and an instruction line
,
and therefore, we can encode the state by
.
Now, let contain the program code, and
contain
the current state. Let
be the first
element of the program state, which tells us, at which position of
we are. Let
be the current
instruction given by
.
- If
, let
and
.
is the value of the
-st register in the simulated program. We replace it inside
by
and replace
by
. We simulated
R[k-1]++. - Similarily, we can simulate
R[k-1]--. - For
, we have to check the register value, and set the instruction number to the apropriate value.
- For
, we end, and have the final state of the program.
While it is really intricate, we can see that it is possible to
"simulate" a register program inside a register program. A natural
question which arises is: Is there an algorithm such that, given a
program (or its Gödelization), and an input state
,
the algorithm determines whether
terminates. This problem
is called the Halting problem. We now show that it cannot be
solved. Formally, we show that there is no program
that,
given the Gödelization of a program
in
and an
input state in
, leaves
being 0 if and only if
with the given input state terminates. We do this by
contradiction: Assume such an M exists. Then we could, from this M,
generate the following program:
"execute M"
if R[2]==0 then goto Loop
End
Loop: goto Loop
This program terminates if and only if the given program with
the given state does not terminate. We modify this program once again
by one line:
"set R[1] to <R[0]>"
"execute M"
if R[3]==0 then goto Loop
End
Loop: goto Loop
We call this program .
only takes one argument. It
terminates if and only if the given program, given its own
Gödelization, does not terminate. Such programs are called
self-accepting.
Now, as is itself a program, we can Gödelize it, so let
be the Gödelization. By setting
, we can
calculate
.
Now assume terminates. This means that in
after
executing M there will be
R[2]==0. Therefore
would not terminate. Contradiction.
But assuming would not terminate would mean, by the same
argument, that
R[2] is not 0 after M. Therefore, would
terminate. Also a contradiction.
Such a program cannot exist. Therefore,
cannot exist.
This proves that we cannot generally decide whether an algorithm terminates. However, it is not yet what we want: We want an algorithm, of which we cannot decide whether it terminates, at all. To get it, we need to do a bit of logic. We will mainly focus on Zermelo-Fraenkel set theory here, as it is the foundation of mathematics.
We first define what a mathematical formula is, which is essentially a string that encodes a mathematical proposition.
- We have an infinite set of variable symbols
.
- The set of strings
is the set of atomic formulae: Formulae which just give them
-relation between two free variables.
Now, the set of formulae is the smallest set, such that
- Every atomic formula is a formula:
.
- If
and
, then
("for all a X holds") and
("there exists an a such that X holds") and
("not X") are in
.
- If
, then
("X and Y"),
("X or Y") and
("X implies Y") are in
.
We now give the axioms of set theory:
NUL: There is an empty set:
We can introduce a common shorthand notation for by
, and rewrite this axiom as
If we want to talk about the empty set now, we need to introduce some
variable , and add
to the
formula. Therefore, our system doesn't get stronger if we introduce a
symbol
for the empty set, instead of always adding
this formula, and it increases readability, which is why we do that.
We furthermore define the shorthand notation
by
, and
by
.
EXT: The axiom of extensionality says that sets that contain the same elements are also contained in the same sets:
FUN: The axiom of foundation says that every set contains a set
that is disjoint to it. From this axiom follows that there are no
infinite -chains.
or, with additional obvious shorthand notation
PAR: The axiom of pairing says that there is a set that contains
at least two given elements, meaning, for all , there
exists a superset of
:
UN: The axiom of union says that the superset of the union of all sets in a set exists:
POW: The axiom of the powerset: A superset of the powerset of every set exists:
.
INF: The axiom of infinity says that a superset of the set of
natural numbers exists. Natural numbers are encoded as ordinals:
, and
. Writing it out
as formula is left as an exercise.
The other two sets of formulae we need are given by axiom schemes: They are infinitely many axioms, but they can be expressed by a simple, finite rule:
SEP: The axiom scheme of separation says that, for every formula
and every set
, the set
exists:
Let a formula be given with free variables among
, and
not occur freely. Then the formula
.
is an axiom of set theory.
RPL: The axiom scheme of replacement is a bit more complicated.
A formula is called a functor on a set
(which is not the same as a functor in category theory), if for all
there is a unique
such that
holds. Therefore, in some sense,
defines something
similar to a function on
, and we write
for this unique
. Then the set
, the "image" of
,
exists. Formalizing this scheme is left as an exercise.
AC: It should be noted that usually the axiom of choice is added. However, we do not need to care whether it is added or not, so we omit it here.
We already talked about embedding natural numbers into this set theory. We can also define general arithmetic inside this set theory. Most of mathematics can be formalized inside Zermelo-Fraenkel set theory.
Now, we can formalize propositions. Now we want to formalize proofs. Normally, I would introduce the calculus of natural deduction here, because it corresponds to the dependently typed lambda calculus, so every proof is a term. However, for the specific purpose we need, namely, formalizing proof theory in arithmetic, the equivalent Hilbert calculus is the better choice. It corresponds to the SKI calculus for proof terms.
Firstly, we further reduce our formulae: We can express
as
, and
as
. Furthermore,
can be expressed by
. Hence, we only need
,
and
to express all formulae. We now
define additional logical axiom schemes, where
range over all formulae. (Notice:
is right-associative.)
- P1.
- P2.
- P3.
- Q5.
for all variables
- Q6.
- Q7.
if
is not free in
A proof of a formula is a finite sequence of formulae
, such that
and for
all
, either
is an axiom of set
theory, or a logical axiom, or there exist
such that
. Essentially this means that
everything in the formula is either an axiom or follows from former
formulae applying modus ponens.
Completeness Theorem: If a formula is true in set
theory, then there exists a proof of it.
To prove this, we would need model theory, which would lead too far, so we leave out the proof.
Now, as we did for programs before, we can gödelize formulae and
proofs. Let us denote by the gödelization of
.
Diagonalization Lemma: For every formula with one
free variable
, there exists a formula
, such
that
holds.
Proof: First, we notice that, given the formula , we
can express the substitution of another variable
for
, therefore, we can give a function that satisfies
. Now we can
define
. Now,
define
. Then we have
. This concludes the proof.
Notice that the definition of is computational: It can
be done effectively by a computer. As we can find such a formula for
every
, we denote it by
.
Now, we can also gödelize proofs and their correctness
criterion. Therefore, we can give a formula meaning
"
is the gödelization of a correct proof of the gödelized
formula
". Therefore,
says
that the gödelized formula
is provable.
By the diagonalization lemma, there is a formula
such that
. Now,
assume that
does not hold. Then
also cannot hold,
therefore, it would be provable, which is a contradiction. Hence,
must hold. But then, it cannot be
provable. This is a (sketch of a) proof of
Gödel's first incompleteness theorem: In Zermelo-Fraenkel set theory, there are propositions that can neither be proved nor disproved.
More generally, this theorem holds for all axiom systems that are capable of basic arithmetic, because this is all we used. Specifically for Zermelo-Fraenkel set theory, there are other examples of such propositions, namely the continuum hypothesis, and the existence of large cardinals.
Now, something we always implicitly assumed is that set theory is
consistent: If is provable, then
cannot be provable. This is, however, unknown, which follows from:
Gödel's second incompleteness theorem: Set theory cannot prove its own consistency.
Proof: We use our from the proof of the
first incompleteness theorem. Furthermore, we can define
such that
. Now, we can
define what it means to be consistent, namely:
. Now, we know that
, and therefore, since
false propositions imply anything,
for all formulae
,
and obviously this implies
. Therefore,
. But this contradicts what
we proved in the first completeness theorem. Hence,
cannot be provable.
Let . Obviously,
if and only if set theory is inconsistent (since it is
wrong). Now consider the following algorithm:
Retry: if ν(R[0], a) then goto Found
R[0]++
goto Retry
Found: end
Does this algorithm terminate?
If it terminates, it has found an inconsistency in set theory. Assuming that set theory is consistent, it would not terminate. But if we could prove that it does not terminate, we would be able to prove that set theory is consistent, and this contradicts the second incompleteness theorem.
Hence, we have an algorithm of which we cannot decide whether it terminates.
Thu, 01 Nov 2018 15:43:26 GMT
Nie dürft ihr so tief sinken, von dem Kakao, durch den man euch zieht, auch noch zu trinken.
- Erich Kästner
So I bought a new smear^H^H^H^H^Hsmartphone. My old phone was fine, it was a Moto G5, but somehow the developers thought that an exchangable battery is an excuse for not including a compass – but I often use it to navigate, and that sucks without a compass. Now I bought a Moto G6, which has a compass, but no easily exchangable battery, and a fingerprint sensor that is even worse than the one from the Moto G5.
Not being able to easily exchange the battery is the current trend. I chose the Moto G6 because at least it seems to be doable to exchange the battery at some point. I want a phone which I can have for longer than two years. And I think one reason for not having an exchangable battery is to make people buy new phones after about two years, because that is usually the time, in my experience, when batteries lost a relevant amount of duration. It is an instance of Planned Obsolescence.
Which brings me right to the point: The whole ecosystem around Android is a big capitalist circlefuck. Android has created an immune system against software freedom and personal freedom.
So when starting my new phone, the shiny motorola start animations shalmed right back at me. Then I was asked to enter my SIM code and connect to Wifi. Then I was asked whether I wanted to import settings from another phone, which I wanted, so I started the procedure and hoped that my app settings would be synced.
After that, I was kindly asked to connect my Google account with Outlook, because reasons. I accidentally did that, now Microsoft can access my Mails from Google I guess(?). Well, why not. I mean, Outlook appears to be the default Mail application on this phone. I have no idea why anyone would want that instead of the original GMail app, but just as a wild guess, one could think of the possibility that Microsoft might have payed for that.
After that, there was a system upgrade, and lots of "system apps" were updated. "System apps" are apps you cannot uninstall. One would assume that these apps are essential for the system to work. But to be honest, I do not see why "LinkedIn" is an essential app. Again, one might think of the possibility that LinkedIn &c payed for that.
Then I was asked to configure the fingerprint reader, and got some messages from these "system apps" telling me that they are there and why I should use them or something … I just closed them. There were two reasons for choosing a Moto G6: The first reason was that I hoped it would be similar to the Moto G5. I don't see that. The UI is entirely different. The second reason is that the older Moto G phones are supported by Lineage OS, so I hope that in the future, it will also be supported. That is important, because the vendors stop supporting their phones at some point – which is also planned obsolescense, but also creates a huge security hazard. There should be laws against this practice – but that will probably not happen in Europe.
Update: I was told that Lineage OS still uses proprietary blobs as its drivers, which may contain security holes but can only be fixed by the companies that made them. Replicant doesn't do that, but won't run on as many devices, therefore.
Now even though I used the official sync functionality, most things just have not been synced. Like, everything useful was not synced. My app settings for Conversations and K9 Mail for example. Also my WhatsApp contacts and logs were not synced. I restored a backup, but only to learn that it lost messages. Because this is not how Android works. In theory, as it is a single-user system, there could be some central place where apps store their configuration. Think of the windows registry or dconf. Instead, apps get their directories in which they place SQLite3 databases.
Which brings me to the next point: The filesystem. Yes, Android has one, but tries to hide it. I do not understand why hiding the filesystem is so trendy right now. Hierarchical filesystems are good, clean, simple and easy to understand. They are a perfect example of an abstraction that is easily usable by humans, as well as efficiently implementable for computers. On Android, it can be hard to create a file with one app, and open it with another app, even though they are on the same computer. This got on my nerves several times. And people start to think it has to be this way. It hasn't. Having access to a cleanly structured filesystem is strictly better than whatever Android does.
And since sending a file to another app on your same phone is so hard, it can be almost impossible to get some file from your computer to your phone (let alone saving it in the right place and making the corresponding apps open it). I have seen people use DropBox for this several times, even though the two computers were in the same room. And for the providers, this makes sense: It makes you use more traffic, and it makes you upload more files, so they can be scanned into your ad profile.
This brings me to another point: The connectivity. It is assumed that you have a fast internet connection with no traffic limits. Many apps assume this. YouTube does not properly cache its videos, except when you explicitly download them. Chrome always reloads tabs when they went out of focus too long. There is no caching done. I have also seen some apps profiling your network connection to decide how much bloat to download. All of this assumes that you have an infinite amount of traffic. But of course, this is good for your internet providers: As there is still no affordable real flatrate for mobile internet in Europe, you will have to pay for additional traffic.
However, still, a smartphone is a highly portable computer, and as such, often changes places, and therefor often switches between networks. That is a problem for chat applications which need to manage their persistent connection. Also, sending keep-alive-packets will drain battery. In theory, TCP with the right parameters should be able to handle this. In practice, programmers do not know this. Hence, Google invented cloud messaging: Your app registers a server, which connects to Google servers, and sends messages. Google play services will itself keep an XMPP-connection to the Google servers, and forward those messages to the registered apps.
The problem is that your app needs to be from Google play. F-Droid apps cannot do this. Another problem is that the push server is hardcoded into the app. That is especially bad for free decentral services like XMPP: I am hosting an XMPP server, and Conversations is a very good client, but the version supporting cloud push costs a few euros, because they have to host an own cloud push server. To prevent this, I would also host an own cloud push server. But to do this, I would need to recompile the app and put it into the Google play store. Which is stupid, considering the fact that it would cost me money, and it would publish my Conversations fork for everyone, while I just want the people with an uxul.de-Account to use it. In the meantime, there might be an alternative, HTML5 Web Push. Maybe there will be support for this in some web client like converse.js in the future. At the moment, there isn't.
The App store is a problem of its own. In theory, having an app store is a good thing. It can improve security, because one can quickly react to security holes. It also can do dependency tracking. In theory, it is like a good old package repository, think of Debian/Ubuntu. In practice, there appears not to be any dependency management, and every app just bundles all of its dependencies, because a few hundred megabytes for a mail client is not a reason not to use it, aparently. Also, it costs money. Not much money, but it costs money. Commercial apps have no problem: Hosting a push server in AWS is cheap. And WhatsApp and Telegram are free as in free beer, and work out of the box.
Of course, they collect your data. Yes, they are encrypted, but at least they know your friends, and they know when you are awake. I would guess that automatically reading your address book entries should be illegal. The Facebook Messenger at least asks whether he may access the address book. They make you the criminal.
Android kills background applications, except when you explicitly allow them to run. This is one further reason for cloud push. And this really gets on my nerves sometimes. I often use Google Maps and the Deutsche-Bahn-Navigator. I want these to stay open, so I can look up things again afterwards. However, it seems that they are reaped from time to time. And they will not always go back to the state where I left them. This is annoying. Of course, you do not have to worry about closing programs anymore, as you would have on a normal computer. But I do not really see the great advantage in that. I also do not see why they do not support swapping.
People often argue that my opinions assume that smartphones are computers. They do. But I don't see why smartphones are not computers. They are small, highly portable computers, with lots of sensors and a touchscreen. The touchscreen is the main difference to laptops and notebooks. And for computers, there is a set of principles that work: The UNIX principles.
Fri, 05 Oct 2018 18:23:32 GMT
External Content not shown. Further Information.
Oh Freude, die Bayern werden ja bald wieder falten gehen. Meine Güte ist das spannend. So viele Themen die mich nicht interessieren.
Der allwissende Wahlomat, der irgendwarum nur acht Parteien auf einmal sortieren kann, sprach zu mir, ich solle grün wählen. Für mich als linksgrünversifften Universitätsgelehrten ist das jetzt nicht so die mega Überraschung gewesen. Aber es erinnert mich an etwas…
Ich befinde mich ja momentan in Baden-Württemberg. Also hab ich mal die lokale Bevölkerung die mir so über den Weg lief gefragt, was sich seit der grünen Machtübernahme so geändert hat. Die Antworten sind alle irgendwo im Spektrum von "meh" bis "Stuttgart 21 something something". Ist ja auch egal.
Gleich danach kommt wenig überraschend die Linke, die sich zumindest bei den gestellten Fragen einfach nicht relevant von den Grünen unterscheidet. Nunja, realistische Regierungsbeteiligung wird die Linke sowieso nicht kriegen. Vermutlich werden alle "etablierten" Fraktionen ihnen genauso bockig wie immer die politische Zusammenarbeit verweigern. No Eisner for you, bitches!
Oh und vermutlich wird auch die 𝕬𝖑𝖙𝖊𝖗𝖓𝖆𝖙𝖎𝖛𝖊 𝖋𝖚𝖊𝖗 𝕯𝖊𝖚𝖙𝖘𝖈𝖍𝖑𝖆𝖓𝖉 ihr Unwesen im Landtag treiben dürfen, an deren Stelle würde ich mir aber ebenfalls wenig Hoffnung auf politische Zusammenarbeit machen.
Ich weiß immernochnicht wie ich zum Verweigern von Zusammenarbeit stehen soll. Irgendwie kann ich es ja ein bisschen verstehen, aber irgendwie finde ich es auch undemokratisch, legitim gewählten Volksvertretern, und damit deren Wählern, die Politikfähigkeit abzusprechen, selbst wenn sie nicht meiner Meinung sind. Aber vielleicht bin ich da auch zu idealistisch.
Da vom Alpenland zum Maine jeder Stamm sich fest vertraut gibt es dann noch ein paar unterschiedlich extreme Frankenparteien wenn ich das grad richtig im Kopf habe. Oh heiliger Veit von Staffelstein.
Oh, und sie haben es geschafft, eine Partei, die selbst für mich zu wenig pragmatisch ist (zumindest bei den Fragen des Wahlomaten) zu erfinden: Die Humanisten. Ich tendiere gerade ein bisschen dazu, diese Partei unter /r/iam14andthisisdeep/ einzuordnen, hatte aber bisher keine Lu^H^HZeit, mich mit ihrem Programm intensiv zu beschäftigen, und lasse mich gerne vom Gegenteil überzeugen. Relevanz werden sie wohl zumindest dieses Mal sowieso nicht haben.
Und es gibt allen Ernstes noch eine Piratenpartei, lolmao.
Nunja. Hoffen wir das Beste. Frohe Arbeit, frohes Feiern, reiche Ernten jedem Gau. Und so.
Sun, 11 Mar 2018 21:21:30 GMT
In theory, XMPP needs no versioning: There is a mighty base-protocol with lots of extensions, and the extensions just need to be negotiated and can then be used. But then again, there are lots of xmpp clients out there with different sets of extensions. Some are older and unmaintained and do not support crucial new XEPs. Some are too new to support all XEPs. Nevertheless, all of them can be called "XMPP Clients". Because "XMPP" is a base-protocol with many extensions.
In my opinion, it would therefore be a good thing to take sets of such XEPs, and define "XMPP Levels" for them. "XMPP Level 1" could be the base protocol, while "XMPP Level 2" could contain the crucial XEPs for modern mobile communication, like Stream Management, Client State Indication, Message Carbons and maybe Cloud Push. Then, clients supporting only Level 1 would still be XMPP Clients, but maintained modern clients which support modern XEPs can call themselves "XMPPL2-Clients".
From a technical perspective, this seems random. But from a user perspective, knowing about "supported XEPs" is not really something desirable, whereas knowing "XMPPL2 New, XMPPL1 Old" is something that can be told to everyone. It would furthermore stigmatize older unmaintained XMPP Clients – which is a good thing in my opinion.
In some situations, some XEPs are not useful. Like for the BitlBee gateway, which is meant to run on servers with high connectivity, Stream Management seems not that important. But then they still could say "XMPPL2 except for Stream Management" – it is clear that especially open source projects will not always be up to date or will sometimes deliberately not comply with such versioning. But it would still be better than today's very chaotic system, in my opinion.
Wed, 28 Feb 2018 19:32:18 GMT
For every tesselation, we can give a graph, which contains the edges and nodes of this tesselation. For example, the graph of the dodecahedron is
It is a graph of the kind 5 3, where every surface has 5 edges, and at every node, 3 edges meet. For 5 3, this graph is finite. For 4 4, this graph is the regular tesselation of the euclidean space:
But, for example, for 3 8, there is no regular tesselation on the euclidean space anymore, and none on the sphere. But there is a regular tesselation of that kind on the hyperbolic space.
Now, I was inspired by HyperRogue to try to produce some code,
without any direct goal. I created a program that generates such
graphs. And for debugging, I wrote a method that creates a
GraphViz definition. GraphViz is a program for layouting graphs;
it has several methods to find good starting points for several types
of graph. When trying the sfdp method (and tuning a bit), I got the
following output:
The documentation says that sfdp tries to arrange the nodes by reducing force (whatever force exactly is in this
case). It cannot arrange the outer nodes anymore, so we get a curly outer line – which reminds me of lettuce (Image
Source: Wikimedia Commons):

Lettuce also approximates hyperbolic surfaces. I am not sure why exactly, but probably to maximize the surface of its leaves. Maybe some similar process is going on in both cases. Or maybe it is just coincidence.
Anyway, I think it is beautiful. :3
Mon, 19 Feb 2018 12:59:38 GMT
I was searching for a tutorial for how to generate hyperbolic tessellations programmatically. Since I found none, I guess it is a worthwile thing to use some of my free time to write about my own approaches. This is not a scientific text. Probably there are better solutions to this, and I would be interested in them, so feel free to comment.
I do not yet have a satisfactory way to give unique coordinates to every tile as for example HyperRogue does. If you know how to do this, feel free to send a comment. It has to do with Coxeter Groups.
We will work on the Poincaré Disk Model. In the poincare disk model, the hyperbolic space is the unit circle, and lines are circles and lines perpendicular to this unit circle.
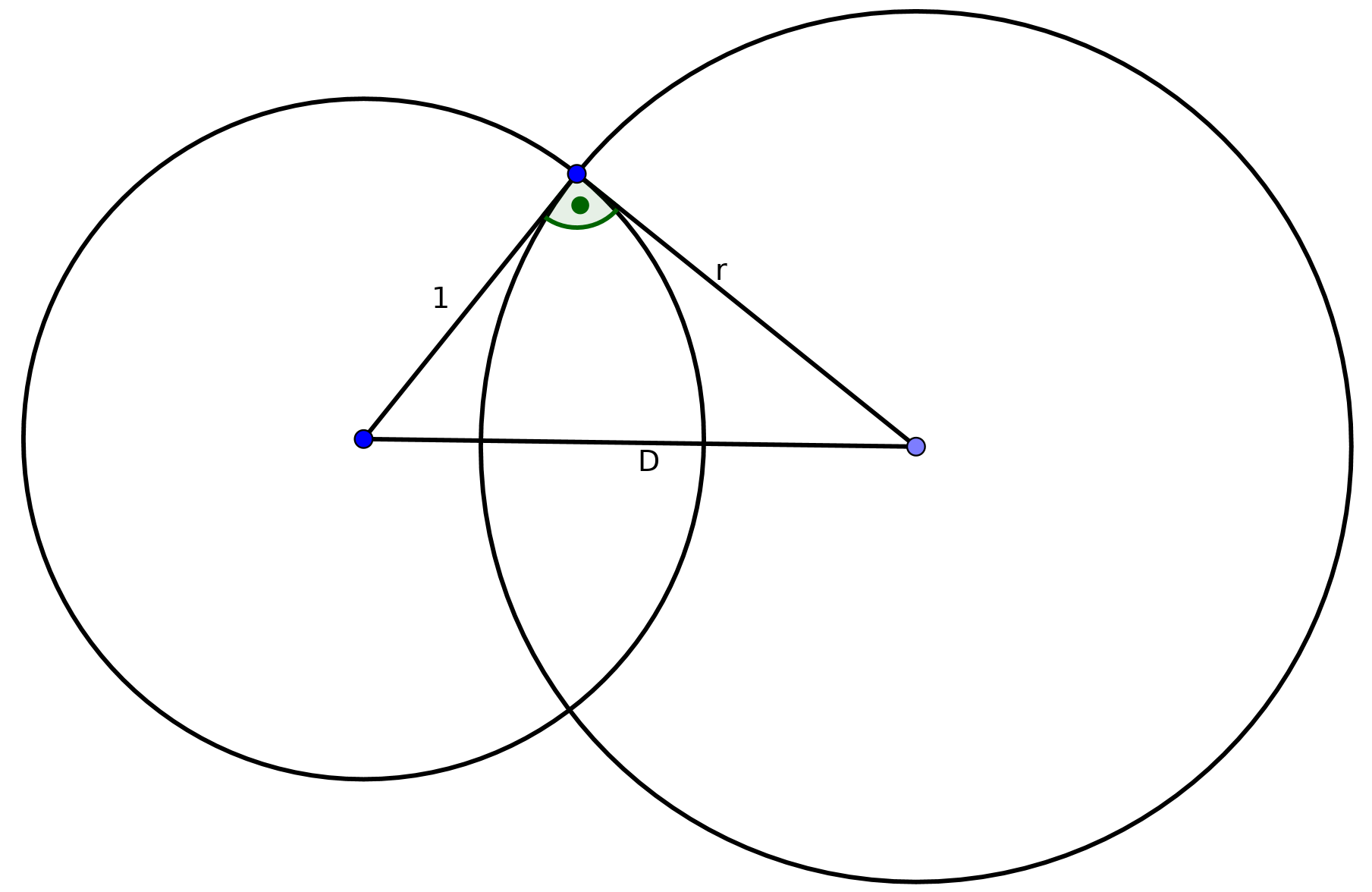
For circles perpendicular to the unit circle, it is easy to see that we have
, where
is the distance between the two centers,
because they form a right-angled triangle. Hence, this holds for every line in
hyperbolic space that is a circle in euclidean space.
If we want to generate a regular tessellation of regular -gons, such
that at every vertex
such
-gons meet, we need to generate an
-gon with inner angle
. We know that the
centers of the hyperbolic lines must form an
-gon in euclidean
space. The side length of the regular
-gon in euclidean space is
.
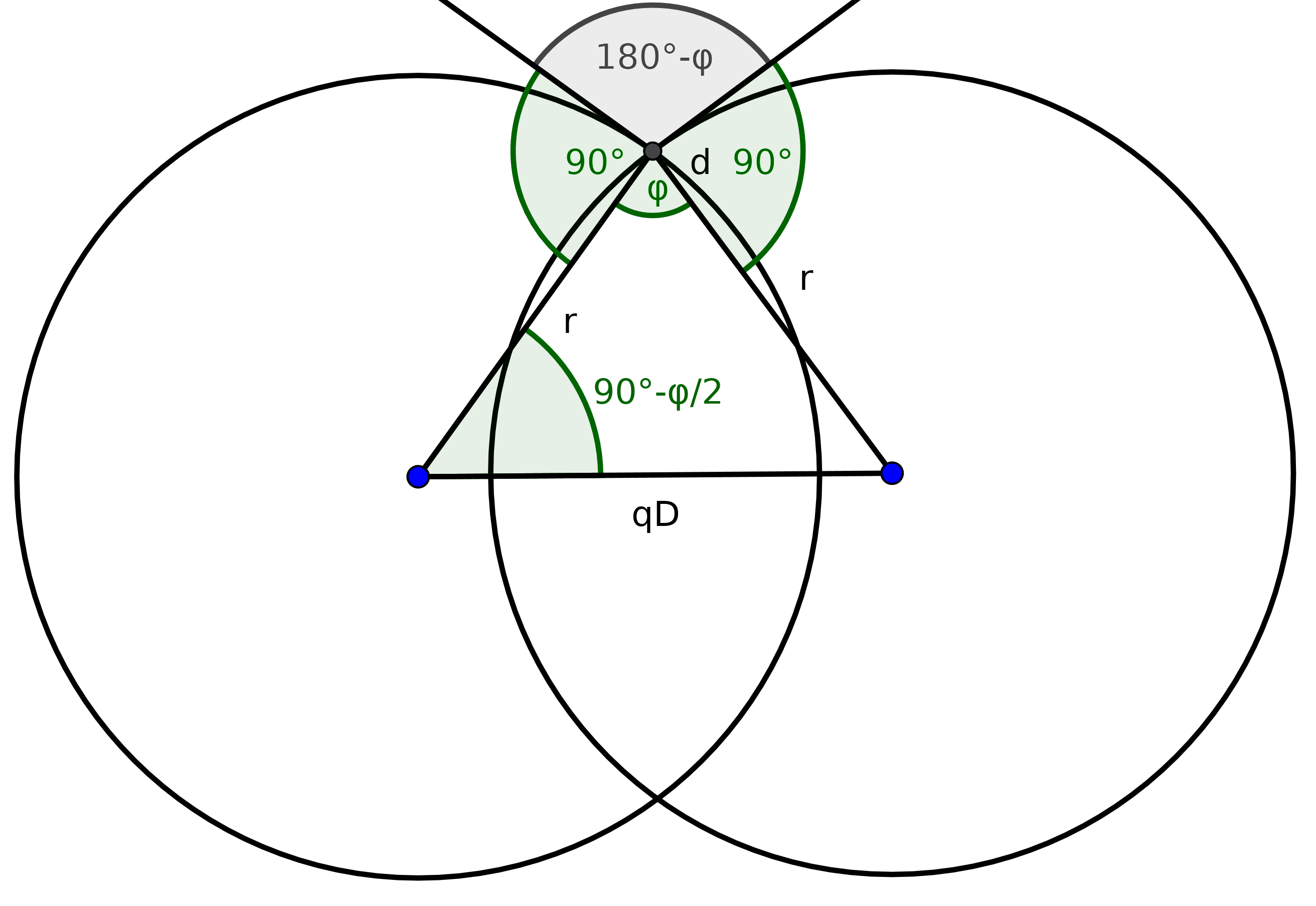
We now consider two such circles. Their center distance should be . Their radii
are equal. Fix one of their two intersection points
and draw the radii through these intersection points. Together with the segment
between their two centers, this forms an isosceles triangle. The angle
between the two radii is complementary to the angle of the
normals through this point, and therefore we know that
. The other two angles in this isosceles triangle, let's call them
, satisfy
.
Now we know by basic trigonometry that the height of the triangle is given by
, and the bottom side
satisfies
.
Inserting the above relation between and
, we get
where
To generate the sides of the polygon, draw circles with radius around
the centers
for
.
To find the vertices of the hyperbolic -gon, just calculate the
intersection points between neighbouring circles, and choose the one with
distance
to the origin. See this thread about how to calculate
intersections.
Fri, 16 Feb 2018 19:23:28 GMT
I HATE BROWSERS! Seriously!
I am used to the following Workflow: I have a feedreader with lots and lots of feeds and I first filter them according to their titles. Everything that sounds interesting will be opened in a new tab. The tabs load, the PC fan spins, and after a while, everything is loaded.
This way, I can load pages before I read them. Loading modern webpages can take seconds, while switching tabs usually took less than a second, and I can do something different while the tabs are loading. Especially when I am in a train, I like to read tabs which have already a loaded website. I usually had a multi-line tab-bar for the about 500 tabs I kept open.
Then, furthermore, I use tabs as bookmarks. I don't really see the big difference – from a user perspective – between bookmarks and tabs. Why the distinction? Why can't I just organize my tabs in groups, which are directories of tabs?
Well, Firefox was never battery saving, but at least it had lots and lots of extensions like, for example, Tab Mix Plus and Tab Groups Manager. Well… Until Mozilla decided to drop support for them. Now, Firefox is just another browser, and especially, it is a browser which does not perform too well. It has an extension Tree Style Tabs which does a good job at organizing tabs.
Palemoon still supports old extensions. I used palemoon for some time. But I am sceptical whether Palemoon will stay tuned with newer web standards and security.
And anyway, both Firefox and Palemoon are rather slow and keep draining my battery.
The obvious alternative to both is Chrom{e,ium} – which performs good for the casual user I guess, but is just terrible at handling many tabs. The tabs will degenerate to small "spikes" when too many are loaded. There are extensions which at least try to be a substitute for tree style tabs, but currently, none of them worked flawlessly for me.
And there is another drawback: Another feature of Firefox is that I could switch to a Socks-Proxy during runtime. This is not possible with Chromium.
I haven't tried Opera for long – it used to be an alternative, but meanwhile it appears like just being a clone of Chrome.
Now I am back at Vivaldi. Which has reasonable tab management in the sense that it at least supports grouping. I configured XFCE to remove the title bars from my windows when they are maximized. Unfortunately, Vivaldi draws its own window borders. You can make it show native window borders, but there will still be a bar above the window when maximized, in which there is only the Vivaldi-Symbol. And when switching to a side-tab-bar, the pinned tabs are expanded. I have openned lots of messengers, so that becomes a problem. Anyway, at least these are just minor UI flaws.
Wed, 13 Sep 2017 19:53:39 GMT
I have a lot of stuff to do recently. So I will pause blogging until about November. See you then, hopefully!