Link List 273
Mon, 19 Mar 2018 20:40:09 GMT

Politics/Law:

Video: Die Grenzen Europas 1000-2013 – wie eine Petrischale.

Nerd Culture:

STEM/MINT:

WTF:

A Shower Curtain That Can Hold Phones And Tablets Is Now A Thing – this will definitely be used to produce amateur porn

Art (Comics etc.):

Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)

Taxus
Tue, 13 Mar 2018 23:02:52 GMT

Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)

XMPP Level 2 (?)
Sun, 11 Mar 2018 21:21:30 GMT

Badly Drawn XMPP Logo eaten by badly drawn flying Uxul.

In theory, XMPP needs no versioning: There is a mighty base-protocol with lots of extensions, and the extensions just need to be negotiated and can then be used. But then again, there are lots of xmpp clients out there with different sets of extensions. Some are older and unmaintained and do not support crucial new XEPs. Some are too new to support all XEPs. Nevertheless, all of them can be called "XMPP Clients". Because "XMPP" is a base-protocol with many extensions.

In my opinion, it would therefore be a good thing to take sets of such XEPs, and define "XMPP Levels" for them. "XMPP Level 1" could be the base protocol, while "XMPP Level 2" could contain the crucial XEPs for modern mobile communication, like Stream Management, Client State Indication, Message Carbons and maybe Cloud Push. Then, clients supporting only Level 1 would still be XMPP Clients, but maintained modern clients which support modern XEPs can call themselves "XMPPL2-Clients".

From a technical perspective, this seems random. But from a user perspective, knowing about "supported XEPs" is not really something desirable, whereas knowing "XMPPL2 New, XMPPL1 Old" is something that can be told to everyone. It would furthermore stigmatize older unmaintained XMPP Clients – which is a good thing in my opinion.

In some situations, some XEPs are not useful. Like for the BitlBee gateway, which is meant to run on servers with high connectivity, Stream Management seems not that important. But then they still could say "XMPPL2 except for Stream Management" – it is clear that especially open source projects will not always be up to date or will sometimes deliberately not comply with such versioning. But it would still be better than today's very chaotic system, in my opinion.

Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)

Link List 272
Sat, 10 Mar 2018 22:21:29 GMT

Politics/Law:

Mehr Penisbilder

Popular Culture:

Nerd Culture:

Deconstructing the water effect in Super Mario Sunshine

STEM/MINT:

Art (Comics etc.):

Refugee

Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)

Predictor
Tue, 06 Mar 2018 19:15:42 GMT

Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)

Link List 271
Sat, 03 Mar 2018 21:36:37 GMT

Hyperbolic 8-3-Tessellation

Popular Culture:

Finanzcheck provoziert mit Kredit-Zinssatz von minus 100 Prozent

Nerd Culture:

Das Xiaomi-Ökosystem vom Hersteller befreien – "Auf dem Staubsauger läuft etwa ein nur wenig angepasstes Ubuntu-Betriebssystem, das auch schnell mit Patches versorgt wird."

STEM/MINT:

Zeroth World/SciFi becoming Reality:

How Disney Rides Know Our Names (via) grusel

Art (Comics etc.):

Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)

Hyperbolic Graphs with GraphViz
Wed, 28 Feb 2018 19:32:18 GMT

For every tesselation, we can give a graph, which contains the edges and nodes of this tesselation. For example, the graph of the dodecahedron is

It is a graph of the kind 5 3, where every surface has 5 edges, and at every node, 3 edges meet. For 5 3, this graph is finite. For 4 4, this graph is the regular tesselation of the euclidean space:

But, for example, for 3 8, there is no regular tesselation on the euclidean space anymore, and none on the sphere. But there is a regular tesselation of that kind on the hyperbolic space.

Now, I was inspired by HyperRogue to try to produce some code, without any direct goal. I created a program that generates such graphs. And for debugging, I wrote a method that creates a GraphViz definition. GraphViz is a program for layouting graphs; it has several methods to find good starting points for several types of graph. When trying the sfdp method (and tuning a bit), I got the following output:

The documentation says that sfdp tries to arrange the nodes by reducing force (whatever force exactly is in this case). It cannot arrange the outer nodes anymore, so we get a curly outer line – which reminds me of lettuce (Image Source: Wikimedia Commons):

Lettuce also approximates hyperbolic surfaces. I am not sure why exactly, but probably to maximize the surface of its leaves. Maybe some similar process is going on in both cases. Or maybe it is just coincidence.

Anyway, I think it is beautiful. :3

Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)

Link List 270
Sun, 25 Feb 2018 07:03:38 GMT

STEM/MINT:

How Should I Get Application Configuration into my Docker Containers?
Möbius Transformations are Isometries of a Sphere
Hotswap Agent – "Java unlimited runtime class and resource redefinition.", also Using HotswapAgent to Speed up Development, also Steps to setup Hotswap Agent in Eclipse
DCEVM – "The purpose of the project is to maintain enhanced class redefinition functionality for OpenJDK HotSpot 7/8 and Oracle JVM."
GiNaCRA is a C++ library providing data structures and algorithms for real algebraic computations.
Going back in (QuickLisp dist) time
ejabberd joins Google Summer of Code 2018
Micro Hydro Power Plant
Riesige Tunnel, die von ausgestorbenen Tieren gegraben wurden
Docker container: Backup and Recovery

Zeroth World/SciFi becoming Reality:

5·10¹¹$-Plan um die Arktis wieder einzufrieren

Art (Comics etc.):

Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)

Hyperbolic Polygons
Mon, 19 Feb 2018 12:59:38 GMT

I was searching for a tutorial for how to generate hyperbolic tessellations programmatically. Since I found none, I guess it is a worthwile thing to use some of my free time to write about my own approaches. This is not a scientific text. Probably there are better solutions to this, and I would be interested in them, so feel free to comment.

I do not yet have a satisfactory way to give unique coordinates to every tile as for example HyperRogue does. If you know how to do this, feel free to send a comment. It has to do with Coxeter Groups.

We will work on the Poincaré Disk Model. In the poincare disk model, the hyperbolic space is the unit circle, and lines are circles and lines perpendicular to this unit circle.

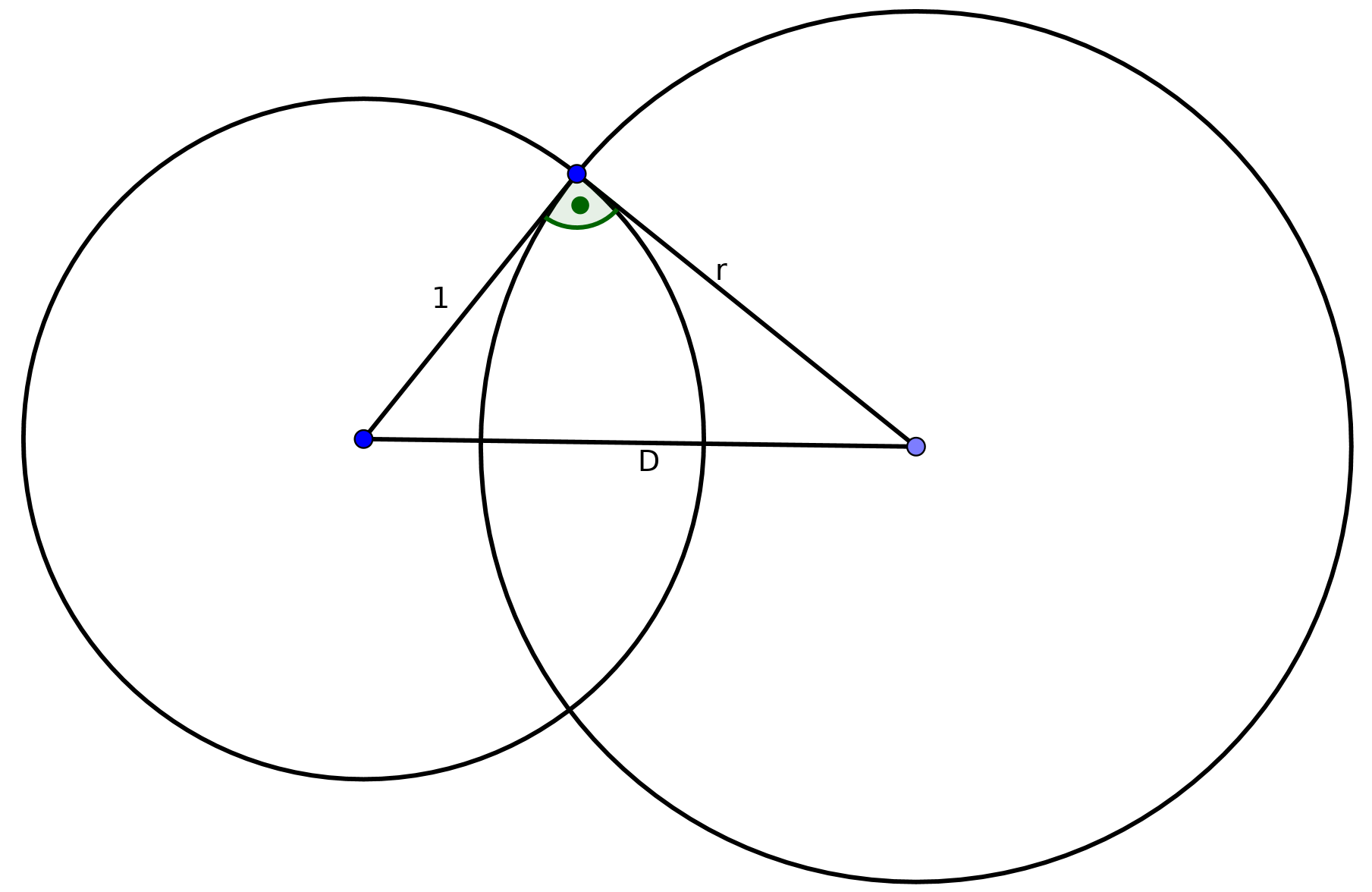
For circles perpendicular to the unit circle, it is easy to see that we have $1+r^2=D^2$ , where $D$ is the distance between the two centers, because they form a right-angled triangle. Hence, this holds for every line in hyperbolic space that is a circle in euclidean space.

If we want to generate a regular tessellation of regular $n$ -gons, such that at every vertex $m$ such $n$ -gons meet, we need to generate an $n$ -gon with inner angle $\alpha = \frac{360^\circ}{m}$ . We know that the centers of the hyperbolic lines must form an $n$ -gon in euclidean space. The side length of the regular $n$ -gon in euclidean space is $q:=2\sin\frac{\pi}{n}$ .

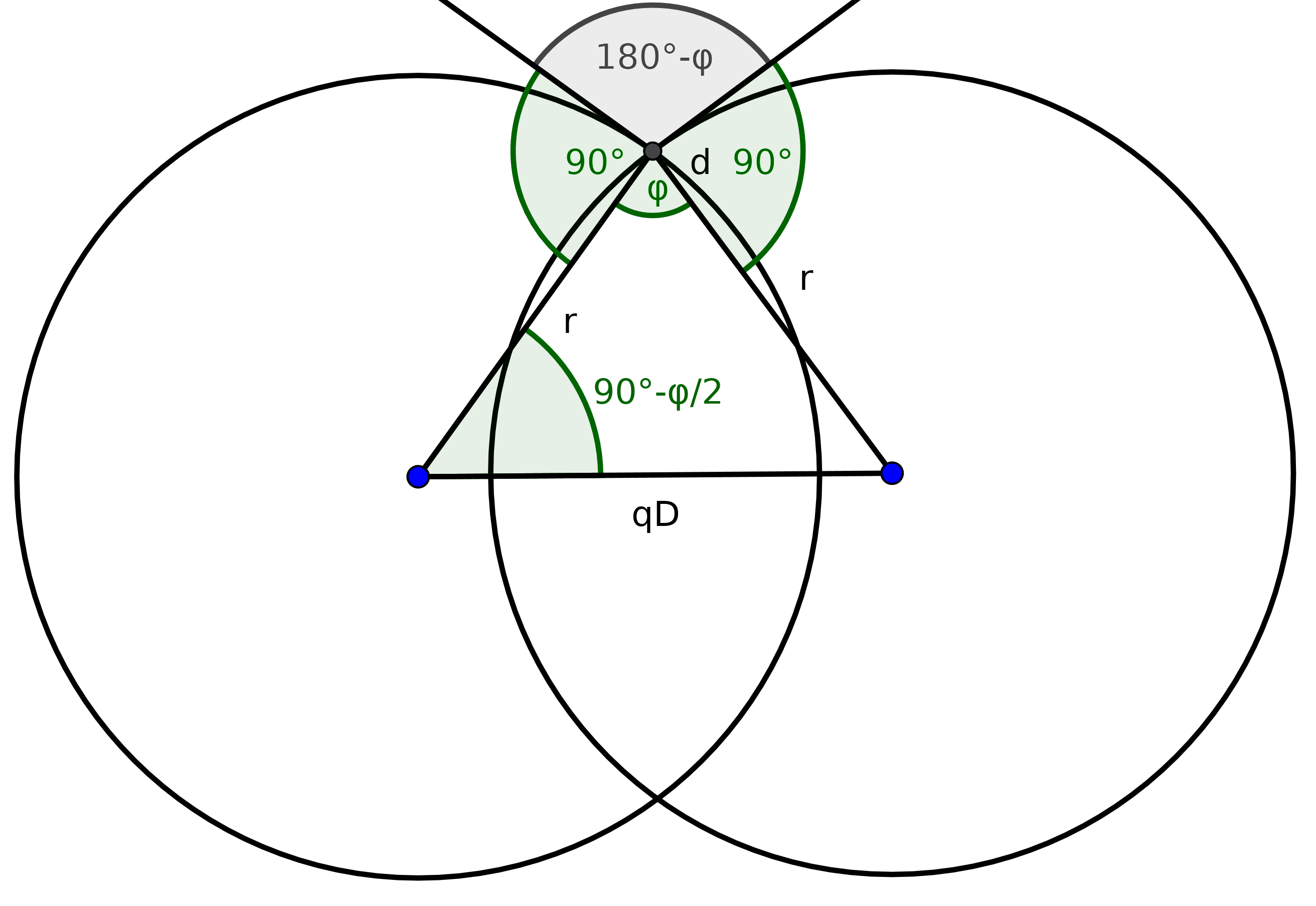
We now consider two such circles. Their center distance should be $q\cdot D$ . Their radii $r$ are equal. Fix one of their two intersection points and draw the radii through these intersection points. Together with the segment between their two centers, this forms an isosceles triangle. The angle $\varphi$ between the two radii is complementary to the angle of the normals through this point, and therefore we know that $\alpha + \varphi = 180^\circ$ . The other two angles in this isosceles triangle, let's call them $\psi$ , satisfy $\psi + \frac{\varphi}{2} = 90^\circ$ .

Now we know by basic trigonometry that the height of the triangle is given by $r\cdot\sin\psi$ , and the bottom side $q\cdot D$ satisfies $\frac{q\cdot D}{2} = r\cdot\cos\psi$ .

Inserting the above relation between $D$ and $r$ , we get

$\frac{q\cdot\sqrt{1+r^2}}{2} = r\cdot\cos\psi$

$\frac{q^2}{4}(1+r^2) = r^2\cdot\cos^2\psi$

$\frac{q^2}{4} = r^2 (\cos^2\psi - \frac{q^2}{4})$

$\frac{q^2}{4\cos^2\psi - q^2} = r^2$

$r = \frac{q}{\sqrt{4\cos^2\psi-q^2}}$

where

$\psi + \frac{\varphi}{2} = 90^\circ$

$\psi + \frac{180^\circ -\alpha}{2} = 90^\circ$

$\psi + 90^\circ - \frac{\alpha}{2} = 90^\circ$

$\psi = \frac{\alpha}{2}$

To generate the sides of the polygon, draw circles with radius $r$ around the centers $(D\cos\frac{2\pi k}{n},D\sin\frac{2\pi k}{n})$ for $n=0,\ldots,n-1$ .

To find the vertices of the hyperbolic $n$ -gon, just calculate the intersection points between neighbouring circles, and choose the one with distance $<1$ to the origin. See this thread about how to calculate intersections.