On Infinity 1 - Introduction and Motivation

Sat, 17 Dec 2011 16:00:00 GMT

Infinity. One central mathematical concept on which many myths have spread, especially in the world outside science. Therefore, I had the idea of writing a series of blog-posts about several aspects of "Infinity".

These posts are not scientific, they are for non-Mathematicians, to demystify the concept of "infinity". But neither is it one of those texts that try to include a lot of "history" and interesting side facts. I just want to give a slight understanding of infinity to non-Mathematicians.

So, in this first post, we shall have a short look at the numbers as such. First, everyone knows the non-negative integers . There are "infinitely many" of them, since every number has a unique successor . This should be intuitive to everybody, and in fact, it is an axiom of arithmetic: Every number has a unique successor. Additionally, we have to postulate that every number except has a predecessor.

Another thing you quickly notice: Take an arbitrary sequence of decreasing non-negative integers (that is, start somewhere, and then "count down", possibly leaving steps out), then this sequence will be of finite length: You will soon or later bump into . A bit more complicated, think of an arbitrary set of non-negative integers. Take, for example, the primes, the odd numbers, the even numbers, the phone numbers of your neighbourhood. You will notice that also every of these sets has a minimal element, even though the set itself may contain infinitely many non-negative integers. That is another axiom of arithmetic: Every non-empty set of non-negative integers has a smallest element.

These two axioms plus the existence of are, in fact, sufficient for elementary arithmetic. A whole lot of theorems can just be implied by these axioms. A simple example: Every number is either of the form or - of course, this is not very profound, it essentially states that every number is odd or even, but we only want to give a simple example. To prove it, assume there was some number which cannot be written in that way, then by our axiom, there exists a minimal such . Since , we know that , and therefore, by axiom, it has a predecessor , and as was the smallest number which can not be written in that form, we know  that there is an such that or . If , then , which we did not allow for . If , then , which is also not allowed. This is a contradiction! So, such a cannot exist: All numbers may be written in that form.


Found at KnowYourMemeNow, of course, there are further objects that are commonly called "numbers". When doing accounting, you are certainly familiar with negative integers. So we get the set of all integers, . They do not share the property that every set of them has a smallest element. There are infinitely many of them into "both sides". So intuitively, there are "more" integers than non-negative integers - of course, the latter is a subset of the first.
But what does it mean for two sets of objects to have the same "number" of elements? Let us first look at the finite case. Let us say you are counting apples. You will take one of them and say "one", then a second one, saying "two", and a third one, saying "three", and so on, until no apple is left that was not counted. Let as assume you counted ten apples. You think you just counted the apples, but what you actually did was giving a one-to-one-mapping between apples and the set . Of course, you probably did not memorize the order you chose the apples - because it does not matter which mapping you chose, the important fact is that there is such a mapping. Such a one-to-one-mapping between two sets is called a bijection. Even in our example, there are many such bijections (calculating the actual number is left as an exercise), and you only chose one by random.

So, for the finite case, we can conclude that two sets have the same number of elements, if there is a bijection between them. For the infinite case, this becomes the definition. Two infinite sets are of equal size, if and only if there is a bijection between them.

Now, let us go back to the integers. We tried to conclude that since the non-negative integers are a subset of the integers, there must be less of them. But on the other hand, define a mapping , that is, is . This is a bijection. So in fact, there are as many non-negative integers, as there are integers at all - even though this might not be intuitive, when looking at the finite case.

In fact, this strange behaviour of infinite sets can be used to classify them: A set is finite if and only if there is no bijection into one of its proper subsets. As there are other (mostly equivalent) definitions of finity and infinity, the concept defined here is sometimes called Dedekind-Finity.


Found at Fukung. This concept is probably hard to understand for a non-Mathematician. The problem is that "finity" is such an intuitive concept, that every non-Mathematician will postulate it was "clear". But this is not the mathematical way of thinking. We will get deeper into this topic in one of the following posts on infinity, when we look at cardinalities. For now, let us get back to numbers.

Of course, even a non-Mathematician knows that there is more than integers. We can extend the numbers to fractions. The set of fractions is called , and it contains all fractions of the form where and are integers, where . Fractions have a nice property: between two distinct fractions, there is always a third one. For example, between and , there is . Even worse, from this directly follows that between two distinct fractions, there are always infinitely many other fractions.

For example, between and , there are the fractions . We have "infinity on finite place", so infinity does not yield distance in any sense. Even worse, we will later show that there is a bijection between integers and fractions: Even though we can squeeze infinitely many of them between and , there are not "more" fractions than integers in the above sense.

As everybody should know from school, every fraction can also be written as a decimal fraction, with either finitely many digits or as a recurring fraction. However, we always find finitely many digits to specify them exactly.

And as many of you will probably know, there are also numbers that do not have this property. For example, , the constant to calculate the area of a circle, has no finite nore a recurring decimal representation, only approximations can be written that way. In general, every infinite sequence of digits which has a dot after finitely many steps can be considered a number, like , , etc., and the set of these numbers are called the real numbers, and their set is called . It can be proved that is actually bigger than . We will later see, how this is done.


Found at Mighty Wombat. Usually, the general education stops at , even though there is a larger set of numbers, the complex numbers, , which many non-Mathematicians do not consider as numbers, because it goes further than what they usually do with numbers. However, it is relevant in science, and mathematically, it is probably more beautiful than . Besides all real numbers, it contains, for example, the imaginary unit , for which we have , it is (one) "square root" of , which we do not have in .


An object which is often associated with is the real line: The real numbers can be considered an infinite line which contains all of them. Then, the following graphic illustrates a bijection between the real numbers between and and all real numbers:



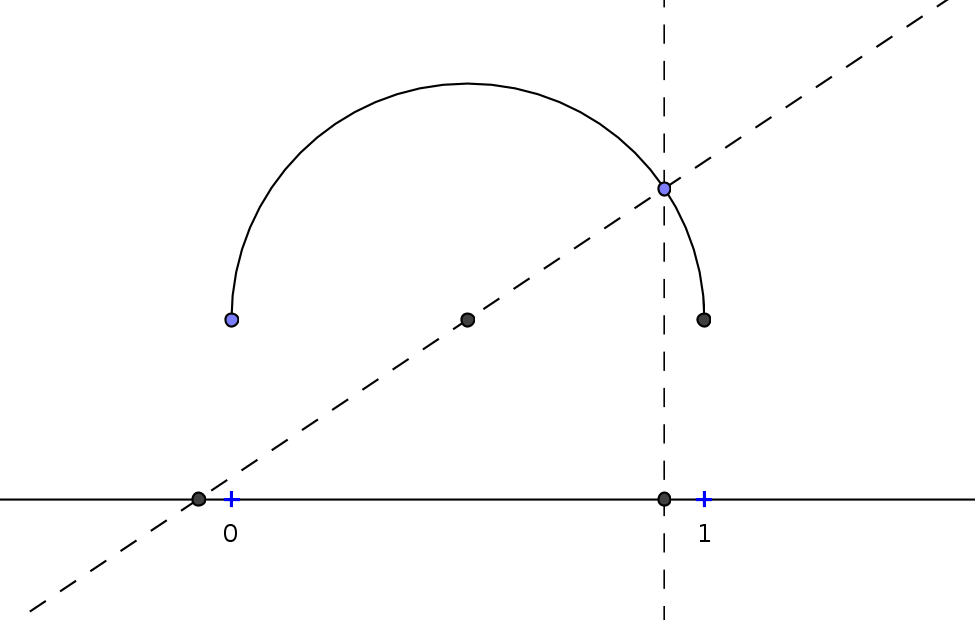
Especially interesting is that and can somehow be considered as the images of the negative and positive "infinity".

So far for this time.