Sun, 25 Dec 2011 23:30:00 GMT
This is the second post of my series on infinity, be sure to read the first one.
We start this chapter with a nice story, "Achilles and the Tortoise", one of Zeno's Paradoxes, though we slightly adapt it. So, Achilles races against a tortoise. He gives the tortoise a 1 mile head start. Assuming Achilles is four times as fast as the tortoise, when he arrives 1 mile, the tortoise is at 1.25 miles. When he arrives 1.25, the tortoise is at 1.3125 miles. When he arrives at 1.3125, the tortoise is at 1.328125. And so on. Whenever Achilles reaches the point the tortoise was when he started, the tortoise already went further. This way, Achilles would have to go through infinitely many points, before reaching the tortoise.
Of course, this is not really a paradoxon. The problem lies in the fact that we have an infinitary process in here. As mathematicians do, we write the problem down more formally. Let be the
be the  -th point where Achilles stands, and
-th point where Achilles stands, and  the point where the tortoise stands. We have
the point where the tortoise stands. We have  and
and  , respectively. By definition, we have
, respectively. By definition, we have  , because Achilles always reaches the former point of the turtle. As the turtle has a 1 mile head start, and has
, because Achilles always reaches the former point of the turtle. As the turtle has a 1 mile head start, and has  times of Achilles' speed, we set
times of Achilles' speed, we set  , which is
, which is  . It is easy to see, that
. It is easy to see, that  , that is,
, that is,  , which is a shorter mathematical notation for such sums.
, which is a shorter mathematical notation for such sums.
Using the axioms we saw in Part 1, we can prove this formally (if you are already a little confused, just skip this proof, it is not necessary for the further understanding): Assume there is an such that
such that  , then there is a smallest such
, then there is a smallest such  . Clearly,
. Clearly,  , so
, so  . Therefore, it has a predecessor
. Therefore, it has a predecessor  , for which we must have
, for which we must have  , since
, since  was minimal. But then,
was minimal. But then,  . Contradiction.
. Contradiction.
Obviously, Achilles will pass the tortoise at some point, and obviously, this point is greater than all . We want to find out more about this point where he passes the tortoise.
. We want to find out more about this point where he passes the tortoise.

The point we are looking for, is . In fact, this is provable. But it is a bit harder than the above induction. What we have here, is a so-called geometric series. As we have
. In fact, this is provable. But it is a bit harder than the above induction. What we have here, is a so-called geometric series. As we have  , we have
, we have  , that is,
, that is,  and
and  differ in the terms
differ in the terms  and
and  , and thus we have
, and thus we have





(source)
We start this chapter with a nice story, "Achilles and the Tortoise", one of Zeno's Paradoxes, though we slightly adapt it. So, Achilles races against a tortoise. He gives the tortoise a 1 mile head start. Assuming Achilles is four times as fast as the tortoise, when he arrives 1 mile, the tortoise is at 1.25 miles. When he arrives 1.25, the tortoise is at 1.3125 miles. When he arrives at 1.3125, the tortoise is at 1.328125. And so on. Whenever Achilles reaches the point the tortoise was when he started, the tortoise already went further. This way, Achilles would have to go through infinitely many points, before reaching the tortoise.
Of course, this is not really a paradoxon. The problem lies in the fact that we have an infinitary process in here. As mathematicians do, we write the problem down more formally. Let
Using the axioms we saw in Part 1, we can prove this formally (if you are already a little confused, just skip this proof, it is not necessary for the further understanding): Assume there is an
Obviously, Achilles will pass the tortoise at some point, and obviously, this point is greater than all

The point we are looking for, is
From this, we see that, the larger  gets, the smaller
gets, the smaller  gets, and therefore, for very large
gets, and therefore, for very large  ,
,  approaches
approaches  . In fact, if we did a little more preliminary work, this would be a valid mathematical proof, and mathematicians would write
. In fact, if we did a little more preliminary work, this would be a valid mathematical proof, and mathematicians would write  , where
, where  is the symbol for "infinity", and call
is the symbol for "infinity", and call  the limit of this series. As we wrote
the limit of this series. As we wrote  for the finite sum, we can also write
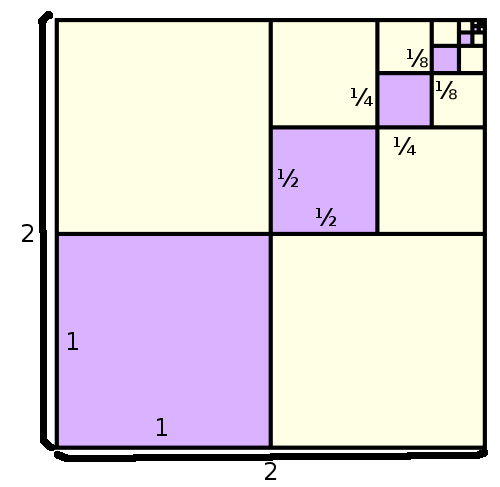
for the finite sum, we can also write  for its limit. The following graphic gives a certain geometric intuition of this fact:
for its limit. The following graphic gives a certain geometric intuition of this fact:

(source)
Of course, it is not always that easy, not every infinite process has a finite outcome. For example, obviously, the infinite sum  does not. However, we know that its finite parts get arbitrarily large, so we might say that
does not. However, we know that its finite parts get arbitrarily large, so we might say that  . This series diverges, while the above geometric series converges.
. This series diverges, while the above geometric series converges.
But even worse, consider the series  . Its finite parts are either
. Its finite parts are either  or
or  . But you cannot find any "tendency" on what happens during infinty. This series neither converges nor diverges.
. But you cannot find any "tendency" on what happens during infinty. This series neither converges nor diverges.  is not well-defined.
is not well-defined.
The above example with the tortoise was one special geometric series, the general (infinite) geometric series is  , which converges for
, which converges for  , and then has the limit
, and then has the limit  - in the case, we had
- in the case, we had  , for a general proof, consider the Wikipedia-article, or any good introduction to calculus.
, for a general proof, consider the Wikipedia-article, or any good introduction to calculus.
Even more general, we have  . With this formula, we can prove a fact quite a lot of people are not willing to understand:
. With this formula, we can prove a fact quite a lot of people are not willing to understand:  , where
, where  means the zero with infinitely many nine-digits after the decimal point. But in fact, we have
means the zero with infinitely many nine-digits after the decimal point. But in fact, we have  , which is
, which is  , which is, according to our formula,
, which is, according to our formula,  .
.
There is a general law about recurring decimal numbers you may know from school, namely,  . For example, from this follows the above,
. For example, from this follows the above,  . More precisely written, we have
. More precisely written, we have  , which follows by our above formula by
, which follows by our above formula by  .
.
As you see, studying this kind of objects can get very complicated, but produces a lot of interesting outcomes. If you did not quite get the last part, do not worry, it is rather sophisticated for a non-mathematician.
Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)