On Infinity 3 - Curves

Tue, 27 Dec 2011 22:00:00 GMT

This is part 3 of my series on infinity.

In part 2 we have seen that there are infinitary processes with a finite outcome. In this part, we will see something, which can at least "philosophically" be considered as the other way around: How to embed infinity into finite objects.

In the end of part 1, we have already seen the following bijection:
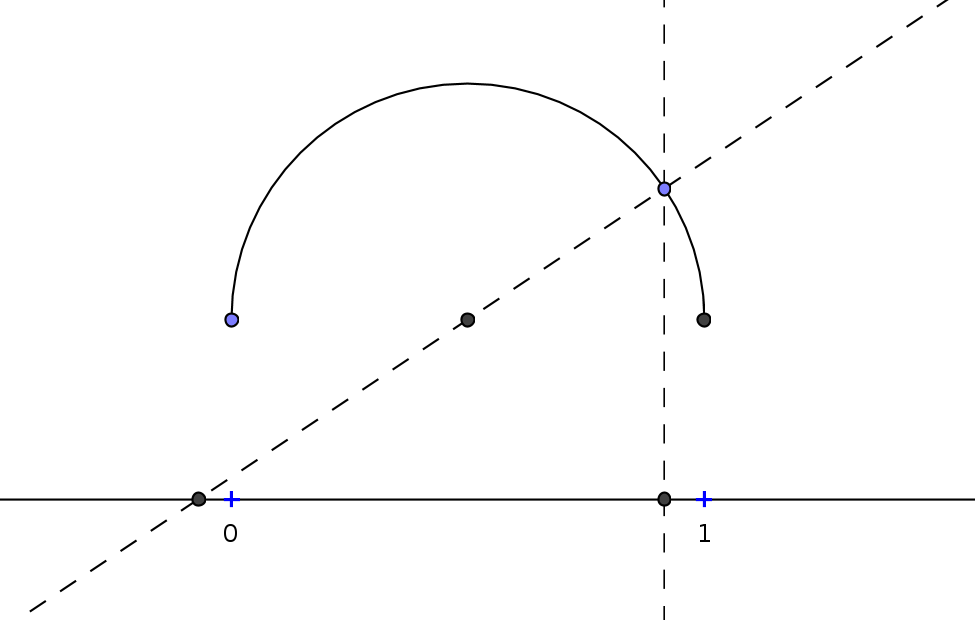
It embeds the whole real line into a finite open interval, so reasonings about the real line become reasonings about this interval, and reasonings about this interval become reasonings about the whole real line. However, this is a bijection, mapping something of infinite length onto something of finite length, but it is not directly something we intuitively consider as an "embedding", and we might ask the question whether it is possible for a finite object to contain a line of infinite length, for example. Now consider the following construction: You start with a square (of side length 1). You cut this square into two halfs, and into the left half, you put an isosceles triangle of height 1 and width 0.5. You cut the other half again into two halfs, and put an isosceles triangle of height 1 and width 0.25 into the left one. Proceed this infinitely often, cutting the right rectangle into two halfs, and embedding an isosceles triangle into the left one. The following graphic shows this:


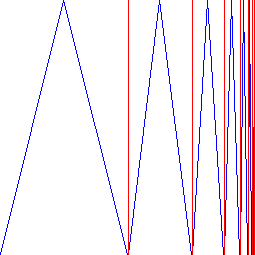
The length of the isosceles lines (blue in the graphic) of the -th triangle have length (which follows by one of Pythagoras' theorems), but the important fact is that it is always strictly greater than , since the height is already , and each of the two lines must trivially be longer. All of the isosceles lines together form a line, the line colored blue in the graphic, and this line must be of infinite length. So in fact, it is possible for a square to contain an infinite line.

Here, the special character of lines must be taken to account: Lines have no width. Lines are ideal objects, which only have a length, but do not have a width. Of course, every line we draw is not ideal, in the sense that - to be able to see it - it needs to have a width. Every line which is actually drawn is only an approximation of lines. Still, the ideal object "line" is not useless: It is a formal object which can be approximated with (probably) arbitrary precision, and its definition was a success and is implicitly used in huge parts of science.

Let us consider another graphic: Assume you draw a square of side length 1. Then centrized into this square, you draw a square of side length 0.5, and inside this, you draw a further square of side length 0.25, and so on. The following graphic shows this:


The circumference of  the -th square has length . So the sum of the lengths is a geometric series, as we saw in Part 2, and we have , that is, all the lines we have drawn together are of length . So, informally speaking, we can draw this "with a pen": We will not need an infinite amount of color to draw it, even though it has infinitely many parts.

So far for this time. We have seen some nice examples of the interplay between finity and infinity, when talking about lengt. Next time it gets a bit harder, we will again look at the countability of sets.