External Content not shown. Further Information.

... was today. I tried to configure a sattelite dish. I found a curious Android app named SatFinderAndroid uses (probably?) GPS and gravity sensors from the phone to find out the relative position of the satellite. The amazing thing: it has a thing called "Sky View", which uses your camera, and shows you the horizon line and the position of the satellite on-the-fly.

Of course, there are other apps, like Sternatlas, that use the same technique.

Fuck yeah! This is amazing. Imagine what else we could do if we managed to develop such technology not only for warfare.

Update: More SciFi-Stuff

Everybody likes "innovation" today. And for the sake of innovation, working pieces of software and well-established standards are sacrificed. Gnome 3 is a good example for seemingly innovative technologies that mainly destroy stuff that used to work well.

However, there is still a lot of place for innvoation which is - unfortunately - often not adressed.

So let me first give you a few examples of things which are not innovative even though often proclaimed.

• Shiny colored buttons which do sounds and have animations when you click on them ~ This worked under Windows 98 already. This is nothing new.
• System-wide file search. Also worked under Windows 98.
• Yet another Widget Toolkit that "embeds" into the L&F of the current system. ~ Mozilla had XUL. Java had AWT. It is good that GTK and Qt are free alternatives that can do this now. Despite, even today many programmers program their own technically bad and optically ephemeral.
• Yet another portable multimedia system ~ Sorry, but for me, mplayer and VLC are the software of choice when playing and recoding music. mencoder and ffmpeg sometimes come. I haven't seen a good free video editor so far, and the commercial ones cost too much and do not run under linux, which is why I still stick with mencoder.
• Yet another runtime framework ~ JRE, Unity, Silverlight, Flash. Let them die and improve HTML5 please.
• Yet another Linux distribution ~ No, we do not need another one. We need a System where everybody easily can write extensions for his special purposes.
• Yet another apps store ~ The nice thing about distributions was that several pieces of software could share common components. "Apps" as such mostly create their own world, and only interact with each other when necessary. This is not a bad thing in general. Especially when someone has to work with multiple versions of the same software, this can become handy. Still, this is just an extension to the Packaging system of a distro. And not just theory.

So here now some things I would really consider "innovative":

• So one thing that really gets on my nerves is that there is still no apropriate way of moving single Windows of Programs to another computer via some remote desktop protocol. In theory, all Systems I know have the technology to do this. There are some problems when it comes to keyboard layouts and accessibility extensions, but in theory, I see no problem to create something like that. And there are lots of remote desktop protocols that allow similar things already, especially NX.
• A VPN that works on all major operating systems, with little configration: You create it, get a key, can request additional pubkeys, and then securely send these pubkeys to the people allowed to access the vpn. I don't see why I need to be a cryptoexpert to create a VPN. SSH is said to be very secure, and is much stronger than a VPN.
• Fewer restarts on kernel upgrades. There are already things like ksplice and kpatch. Same for library upgrades in general: There shouldn't be a need to restart a daemon completely just because a small part of its library changed. This is hard to achieve, of course. But innovations are supposed to be hard to achieve, otherwise they are just "nice ideas".
• "Forks" of my system state. I can suspend to disk. Why can't I resume from the same state twice? Like I can do with clones of virtual machines. I see no reason. One could even go further and trigger automatic system snapshots every 30 minutes. And allowing this for single processes or process groups would make it easier for programmers to make backups for the case of a crash.
• Similar, it should be possible to suspend a process group, and revive it on another computer. At least as long as it is run in some compatibility mode, this should be possible. Of course, several processors differ. Well, it's not easy, but I think it is possible.
• It's time for a system-wide GC. So many Frameworks use garbage collection, and some of them do it in a very bad way. The System knows when it needs memory, and where it needs it. By defining a protocol such that the kernel can take care about it (or let an userspace driver take care about it), it is probably possible to improve the performance of a system on the whole.
• It's time for a higher-level ABI. Dynamic libraries should not only save their names, but also the size of their arguments. Maybe even their argument names. They should specify whether they "swallow" memory so one does not have to free it, or you have to take care of the memory to be freed again. There is a hole lot of stuff that could be saved without any relevant overhead. There should furthermore be standards for overloaded functions. A common name-mangling-scheme for example.
• Why do we bother about window managers so much? This is the 21st century! Hercle! Give me a simple API, make that JavaScript if you really like it most (or make the API portable, even better), and let me tile and style my windows the way I want them to be.
• Keybindings and keyboard shortcuts really get on my nerves. Why can't we finally put a layer between the scan-codes of the keyboard and the actual program in which we can define shortcuts directly, so the software using it gets commands directly instead of ascii characters and modifier masks? One can define commands like "copy" and "paste", as well as more sophisticated commands for special software inside some namespace, like "emacs.proofgeneral.checkproof", and of course, "keypress" per default. This would provide a more common look-and-feel, and finally remove the disadvantages of having alternative editors like Emacs and VIM.

There is a lot of stuff I could add to this list, but that is what currently comes into my mind. These would be the things that I liked. I am not asking anyone to actually make them. I just ask you tu stop destroying working infrastructure, and if you desperately want to produce something, then do something useful instead.

Though fortunately I am not disabled (at least as far as I know), recently I started to take interest in accessibility of software (you might have noticed that most of my comics have a reasonable alt-text now). We are already an information society, we can send information around the globe in milliseconds. We can share our ideas, and even go beyond reality.

And still, it is a pain in the ass to use a bootloader on an ordinary laptop without having a screen. Debian recommends Petitboot - at least it has some alternative.

In the GRUB Git Repo there is has an unfinished branch for BrlTTY support, and while I understand that for a bootloader it is not a trivial thing to support USB Braille Readers, it has a whole shitload of graphic options which are useless, and only there for eyecandy. If at least they would support a screen magnifier or something.

The whole framebuffer-crap is annoying anyway, especially since most linux distros began to make it their default configuration. The default text interfaces worked everywhere and were simple - of course, this had to be changed, so now you have to sledgehammer the default installers before you can use them on old computers with a low screen resolution. We lost backward-compatibility, but what did we gain except eyecandy and a lot of crashes on old hardware? And how much time that could have been invested in more useful things was wasted for that shit?

So now, back to topic. I was trying to find an accessible way to install Ubuntu 12.04 on an encrypted LUKS-root-partition. While a few years ago this was an exotic setup, having an encrypted LVM including swap and root is a default setup now, in my opinion, and I would recommend it to everyone.

Before I go on, when I was talking about writing this post, I was told to mention that the installation process for Windows is completely inaccessible. And yes, Ubuntu does a lot of things right. My aim is to give constructive criticism! Accessibility is not a feature, not being accessible is a bug.

The default Ubuntu Desktop 12.04 installer appears to ... sort of ... work - as long as you use the default partition layout. The partition editor makes no sense when using Orca. This is a major bug in my opinion. But as it does not support root-encryption anyway, I don't care at the moment.

The alternate installer uses Partman, which is a good piece of software, in my opinion. In theory, the installer should be accessible through BrlTTY, but it always crashes. I guess this is a bug, and I will file it.

The installer bases on Dialog, and for me, using it with a braille line is a pain, and I wonder whether it was possible to write a really accessible version of dialog, but other people using it seem to be satisfied with it as it is now. So be it, there are more important things to do, I guess.

As a conclusion, I can say that I currently could not find any accessible way of doing this installation for Ubuntu 12.04, without changing the installer (using preseed-magic, etc.).

However, the same does not hold for the Ubuntu 14.04 previews I tried.

Debian has a nice installer that uses speakup. There is still a lot of room for improvements, but at least it is there.

So well ... it could be better, but it could also be worse, I guess.

I guess the main problem with the installers can be summarized by one sentence from the presentation "Freedom #0 For Everybody Really?", which is interesting to watch anyway: Don't make software accessible, write accessible software.

Ich wurde heute am Stand einer unbedeutenden Kleinstpartei gefragt, auf welcher Seite ich stünde, Edward Snowden oder Obama. "Edward Snowden, kennen Sie?" - natürlich. Wie dem auch sei. Den Inhalt des Gesprächs würde ich unterhalb der Grundschule ansetzen, man konnte mir außer dass Obama die Verfassung™ gebrochen hätte nicht so genau sagen, warum die eigentlich Gegner sind, und was sie eigentlich genau machen.

Wie auch immer. Auf den augenscheinlich mit Packband, Klopapier, ein paar schlecht gedruckten Fotos und Eddingstiften hergestellten Plakaten stand unter Anderem Werbung für Atomkraft und das chinesische Raumfahrtprogramm. So ganz habe ich die Aussage nicht verstanden, und was sie mit Edward Snowden versus Obama zu tun haben soll auch nicht.

Es handelt sich hier aber, denke ich, um etwas, das ich mal als Polit-Parasitismus bezeichne. Eine Kleinstpartei reitet auf einer Empörungswelle, und identifiziert sich mit den Guten™. Der Piratenpartei und den Grünen kann man dies in ihrer Entstehung auch vorwerfen, aber sie sind wenigstens aus expliziten Gegenbewegungen entstanden. Jene Kleinstpartei reitet, ohne wirklich inhaltlich damit zu tun zu haben.

Die Großparteien sind natürlich im Prinzip nicht besser, aber wenigstens muss ich mich mit deren Programm nicht auseinandersetzen und weiß was sie ungefähr machen, wenn sie mal was machen.

As I find that there is a lack of documentation on how to configure and test the braille output of programs, I will give a short overview on how I set up qemu and a virtual braille line for sighted people. This information is probably not relevant for visually impaired people who use a real braille line anyway.

As for all tutorials about software that is not widely used, it will probably not work for you, but hopefully give you useful hints on how to make it work. If you find some mistake or something that could be more clear or something outdated, send me an E-Mail.

I use XUbuntu 12.04 LTS. Even though it is still supported, it is slightly outdated, even for today, but I guess that similar things can be done for newer releases. I will maybe give some update here for the linux system I will use after the support of 12.04 ends. Just feel free to send me an E-Mail in case I forget to do so.

A warning: This is a guide for advanced users! Think before you do anything, and do not do it if you are not sure about it. It is also likely that I have installed some tools that do not belong to the default installation of Xubuntu, but should be easily installable.

One main problem is that qemu changes its commandline arguments from time to time. So this information might be outdated. The other one is that Ubuntu is good at removing features of software without warning or providing alternatives. I had to recompile kvm myself with brlapi-support.

Of course, as a first step, you need brltty to be installed. Furthermore, you need to install libbrlapi-dev. And you need the source repositories in your /etc/apt/sources.lst, which Ubuntu usually omits for ... whatever reason. These are the lines beginning with deb-src instead of just deb, but otherwise look similar.

Now create some directory (the process of recompiling is "dirty" and creates a lot of files in this directory, this is why you want an own directory for that) and run

apt-get source kvm

It should download some stuff and create a subdirectory that is called like qemu-kvm-1.0+noroms or something. In this directory, there is a configure script. When you run

./configure --help

you should find an option --enable-brlapi. This is the option we will use. There is a debian subdirectory, with a file called rules. Open this file in an editor. This file tells what has to be done to build the package, and we have to add this option to the part that runs the configure-script. Now, there are probably many better ways to do this, but here is what I did: I went to the part that starts with

config-host.mak: $(QUILT_STAMPFN)

and added the option:

config-host.mak: $(QUILT_STAMPFN)
        dh_testdir
        ./configure \
            --target-list="x86_64-softmmu i386-softmmu x86_64-linux-user i386-linux-user" \
            --prefix=/usr \
            --interp-prefix=/etc/qemu-binfmt/%M \
            --disable-blobs \
            --disable-strip \
            --enable-brlapi \
            --sysconfdir=/etc \
        --enable-rbd \
            $(conf_arch)

Back to the qemu-kvm-1.0+noroms directory (or whatever it is called for you), run

dpkg-buildpackage -rfakeroot

It will complain about some build-dependencies that are not installed. Install them and run it again. Then wait and pray. There will occur a few warnings that the stuff could not be authenticated because you do not have the maintainer's key, but we just ignore that.

If everything goes right, the parent directory should now contain a few .deb files. Make sure that you uninstalled everything related to qemu and qemu-kvm and kvm before, and install these packages using

dpkg --install *.deb

Hopefully, the software runs now. At least it did for me.

Now grab some linux cd (I used debian-7.3.0-amd64-netinst.iso) and create, as usual, a hard disk image (I called it debian.qcow2). At another shell, run

sudo brltty -n -b xw -B model=vs -x no -A auth=none,host=127.0.0.1:1

You should hear an audible signal, and a window resembling a braille line should appear on your desktop. Furthermore, run

BRLAPI_HOST=127.0.0.1:1 kvm -usbdevice braille -cdrom debian-7.3.0-amd64-netinst.iso -hda debian.qcow2

to start the virtual machine. The stdout of brltty should tell you something like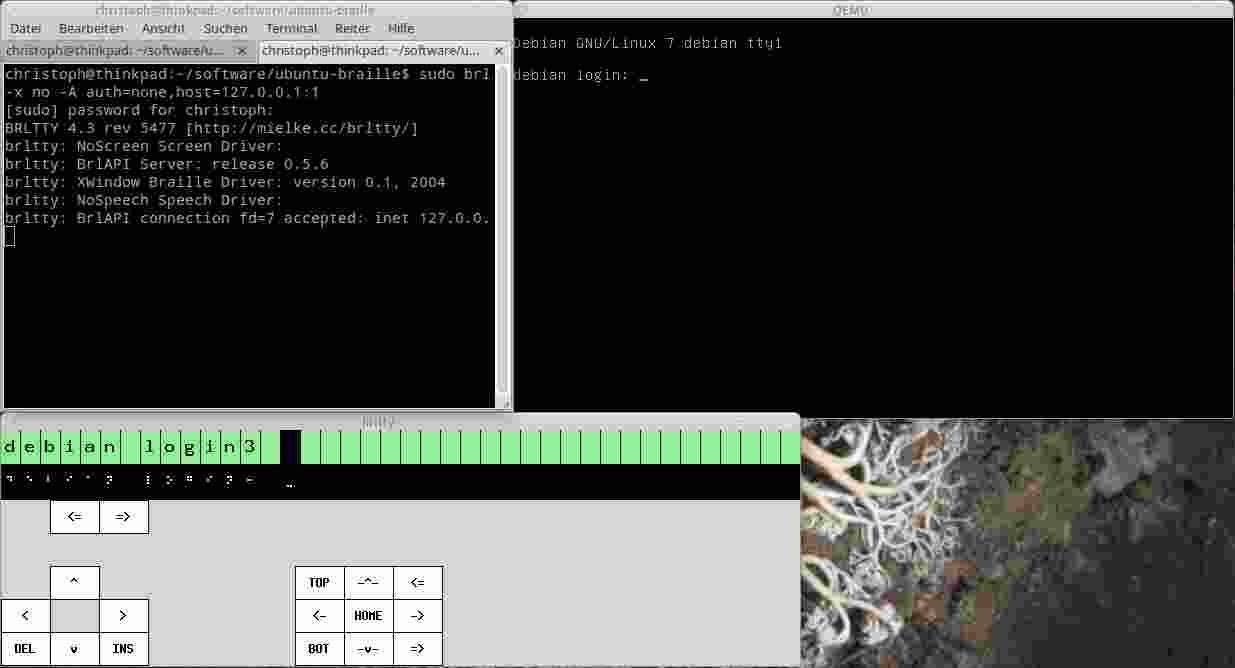

BRLTTY 4.3 rev 5477 [http://mielke.cc/brltty/]
brltty: NoScreen Screen Driver:
brltty: BrlAPI Server: release 0.5.6
brltty: XWindow Braille Driver: version 0.1, 2004
brltty: NoSpeech Speech Driver:
brltty: BrlAPI connection fd=7 accepted: inet 127.0.0.1:47172

If that is the case, it should be connected. The debian installation without looking at the screen is ... hilarious. If I didn't already know it by heart, I wouldn't have had a chance to install it.

Anyway, back to topic: Ubuntu now tries to convince me that the package I created can be updated by the default package from Ubuntu. I hope that it is sufficient to set this package on "hold", which can be done under aptitude by selecting it and pressing =. A better solution would probably be to rename the package and make it collide with the original kvm, or use apt-pinning, but I am currently too lazy to do so.

Consider reading DebianInstaller Accessibility which gives some of this information. I also found Testing accessibility of text applications, but did not try it. Here is some thread in some mailing list that also describes a bit of that stuff.

So. Schaun wir uns erstmal meine Prognosen für 2013 an.

Politik:

• Die Bundesregierung hat zusammengehalten.
• FDP und Piraten scheiterten an der 5%-Hürde, die Piraten aber (leider) nicht nur knapp.
• Große Koalition mit Angela Merkel als Kanzlerin haben wir.
• Was aus der NPD geworden ist, weiß ich nicht. Irgendwelche Äpfel fielen neulich davon ab, soweit ich das mitbekam.
• Fremdenfeindlichkeit nimmt grade zu, kann man wohl sagen. Das ganze Gelaber um Flüchtlinge, Anschläge aufs deutsche Konsulat, und die CSU mit ihrer Angst vor Armutsmigration, kann man wohl so bezeichnen.
• Genitalverstümmelung kleiner Jungen wurde erlaubt.

Kunst und Populärkultur:

• Der Star Trek-Film hat sich nicht verspätet soweit ich weiß. Aber er wurde ein Erfolg.
• Ein richtig neuer Zelda-Teil für die Wii U wurde nicht angekündigt, aber Hyrule Warriors.
• Ein Portal-Teil wurde leider nicht angekündigt, meines Wissens.

Software und Technik:

• Windows 8 kam raus, aber als Erfolg würd ichs nicht bezeichnen.
• Zum iPod weiß ich nichts.
• Weezy wurde stable.
• Boot To Gecko ging in Firefox OS über, im weitesten Sinne stimmt also die Prognose.
• CLang unterstützt glaub ich C++11 inzwischen (zu faul nachzuschauen), und MSVC++ auch, wenn ich mich recht entsinne. Man korrigiere mich falls ich mich irre.
• Ein Projekt ext5 ist mir nicht bekannt.

Wissenschaft:

• P ungleich NP wurde nicht bewiesen, soweit mir bekannt.
• Auch ein Durchbruch bei superluminaren Effekten ist mir nicht bekannt.
• Die Aussage zur Collatz-Vermutung kann, wie man mir inzwischen sagte, garnicht zutreffen.

Sostiges:

• Die Welt ging nicht unter.
• Das Wetter ist zumindest insofern extrem, dass der Winter bisher ziemlich Mild ist.
• Dieses Jahr gab es irgendwie keine Sommerlochseuche.

Tja. Und nun die Prognosen für 2014:

Politik:

• Mehr Überwachung.
• Probleme mit den Flüchtlingswellen, allerdings nichts was es nicht schon mal gab.
• Edward Snowden wird von Obama eine Amnestie erhalten, mit der Bitte um ein Gespräch.

Kunst und Populärkultur:

• Michael Schumacher wird vermutlich leider bleibende Schäden davontragen, aber überleben (gute Besserung an dieser Stelle). Hoffentlich wird er seine Bekanntheit daraufhin nutzen um das Bewusstsein für solche Dinge zu erhöhen, und die Gesamtsituation zu verbessern.
• Besagtes "Hyrule Warriors" wird veröffentlicht werden.

Software und Technik:

• Firefox OS wird sich weiter verbreiten.
• Emscripten wird sich weiter verbreiten, und zum Beispiel benutzt, um einige Webapplikationen zu schreiben.

Wissenschaft:

• Die ersten Exoskelette als Ersatz für Rollstühle gehen in Serie. Leider dauert es noch, bis sie wirklich Verbreitung finden.
• Es wird erstmals erfolgreich gelingen, das Rückenmark eines Menschen partiell wieder zusammenwachsen zu lassen (als Fortsetzung der betreffenden Rattenforschung).

Sonstiges:

• Sommerlochseuche, kein Weltuntergang, irgendwie extremes wetter. Das Übliche halt.

So I was buying Vitelottes.

Then I put them in a bucket with potting soil. Except for an infection with plant lice and watering them from time to time, I mainly had to wait. Then a few days ago, I dug them out. I found some nice things, like this huge maggot:

It might become a chafer - I am not sure about its species, if somebody knows, feel free to send me an e-mail. I just covered it with soil again, after digging out the potatoes. Speaking of which:

Sorry for the bad quality of the photos.

I would call that a success.

Foreword

Again, a talk for the best mathematics club of the multiverse, for the pupils who do not yet study mathematics. This talk has very low requirements and is not thought for mathematicians, but for people who may become mathematicians. It is about basic coding theory, nothing too deep, but hopefully interesting anyway.

Checksums

It happens often that one needs to type in a number somewhere. Several things can go wrong. To prevent this, one often adds some redundancy to these numbers, so it is less probable to make a mistake without noticing.

A famous example are ISBNs. They have ten digits where is usually denoted as . The rule for such an ISBN is now that , which can always be achieved by choosing correctly. The most common errors are single wrong digits, and digit-twists.

Proposition: Two distinct ISBNs differ in at least two digits.

Proof: Assume not. Consider the two ISBNs and such that except for exactly one . Then , but notice that this number cannot be divisible by , since all of its factors are smaller than and is a prime number. But the difference of -divisible numbers must be -divisible. Contradiction. --

Thus, if we got only one digit wrong, we can recover the original code. Of course, if more than one digit is wrong, this does not help. For twists of two adjacent digits, we have

Proposition: Two distinct ISBNs cannot differ only in two adjacent digits.

Proof: Again, consider the two ISBNs and such that for all except for , for which we have and vice versa. Then again, and that can again not be divisible by 11. Contradiction. --

While it is pretty easy to include such an error correcting code, most numbers humans use directly in real life do not use one, probably because people do not know that they exist. (At least I doubt that coding theory is a part of most engineering studies.) While ISBN Codes are widely used, this is of course only a minor feature, and for example, you usually have the name of the book given.

One example from technology that is widely used are the RAID-Systems, Redundant Arrays of Inexpensive Disks. The problem with hard disks is that they have a lot of pretty small technology, and their lifetime is limited. While on personal computers, it is sufficient to make regular backups, in data centers you need more reliability: You do not want to have long pauses or a complicated procedure if one of your disks fails.

The RAID-Systems work on a very low level of data, below the file system and partition table: RAID-Systems work with the bit-sequence, the "zeroes and ones", that are saved on the disk. Therefore, as one drawback, the disks must be of equal size. In practice, they are usually identical in construction.

The easiest way to do this is to just "mirror" a disk: You work with two disks that always save exactly the same thing, and if one disk fails, you just replace it and copy the data from the others. So at every time, you have two bit sequences and , where is the number of bits that can be saved on that disks, and where . If, say, the -disk breaks, the system continues to function, only using the -disk, and as soon as a new -disk is inserted, the whole content of is copied. This is called RAID 1. You need twice as much disks to gain security.

But we can do better, using parity checks. Let us say you have three disks , and again with the bit sequences . We now define a "virtual" bit sequence such that and for all , thus "merging" the bit sequences and . The computer works on this bit sequence , thus seeing a virtual hard disk twice the size of one of the three disks we used. For the third disk, we define that it has to satisfy . The computer maintains this invariant. Now, if breaks, it can just be recalculated from and . The more interesting part is when one of the other disks breaks. Assume breaks, but and still work. As long as we want to read , we can just read . If we want to read , we have to recover the value of . But we know that , therefore . Since , this is the same as , and therefore, we can recalculate , as long as we have and . Compared to simply mirroring, where we need twice as much memory, here we only need times as much memory, but of course, only one out of your three disks may fail. is called the parity disk, because it saves the parities of the sums of the bits of the other disks. In the same way, you can use more than three disks and recover transparently if exactly one of them fails. Which one you choose depends on how much you actually trust your disks. RAID Systems are a way of making data loss less probable, but not impossible.

Parity checks are simple, but they have one major disadvantage: You have to know which of the disks is broken. This is the fact when some essential part of a disk is broken. However, you might as well just have parts of a disk returning wrong data. You can then use Hamming-codes, which scale for large bit numbers, but not for small ones. Therefore, in practice, they are rarely used for RAID systems, since there are better possibilities in this particular use case of only few disks on which you have random access. The practical use-case of Hamming-codes is for sending data over an unreliable channel, for example through atmospheric disturbances. The central idea is to cover subsets of the data bits by multiple parity bits. Assume we have bits . We look at the binary representation of the indices , from to . Every such that has exactly one in its binary representation is used as a parity bit, thus, we have the parity bits . All the other bits are data bits, so we have an overhead of . Now the parity bit describes the parity of the sum of all bits with the binary digit that is set in is also set. For example, is the sum of ,,,,,,, all the indices have the second-least binary digits set. Therefore, by knowing which of the parity bits are wrong, we know which bit is wrong, assuming at most one bit flipped: If only one parity bit is wrong, the bit itself must be wrong. If more than one parity bit wrong, we can restore the binary representation of the index of the flipped bit. Of course, the same works for other bit numbers. Hamming codes also work for higher bit numbers. In general, by the same procedure, we can recognize a single bit failure in a chunk of bits by using bits as parity bits, and bits as data bits.

While having error correction might sound desirable, in cryptographic applications it is often desirable to have error-detection, but no possibility of error-correction. A common problem on webservers is that it must store the users' passwords in some secure way. On the other hand, no server is absolutely secure, and if data is leaked, the hacker can read the users' passwords. On the one hand, this is bad because users tend to use the same passwords for many services, on the other hand, if such leaks are not noticed, the thief can use the cleartext passwords and use the usual logins. In general, Cryptographic checksums of the passwords should be used. Famous examples are md5 (which is obsolete for this purpose) and sha512.

Compression

Most data we work with contains a lot of redundancy. From a purely theoretical point of view, for every machine model and every chunk of data, there exists a minimal representation (see for example Kolmogorov Complexity). However, this minimal representation can usually not be calculated. In practice, approximations are used. For some special purposes, there can be lossy compression, for example, ogg vorbis and theora for audio and video compression. We will only look at lossless compression: The data can be recovered as it was before.

The easiest such compression method is run-length encoding, RLE. In its simplest form, it is basically saving repetitive sequences of characters only once with their multiplicity. For example, in many graphics, you have a lot of singly-colored background, that is, a lot of equally colored pixels. As a simple example, say we have sequences of bytes (values from to ), in which long subsequences consisting of zeroes occur. We can then say that instead of saving the sequence of zeroes, we save only one zero and let the following byte denote the number of zeroes that follow this one. That is, if we have , we can instead save . We then save a sequence of consecutive zeroes with only two bytes. On the other hand, if we have only one zero to save, we need two zeroes instead of just one. For example, the sequence becomes , which needs more memory. A simple pigeonhole argument shows that this must be the case in every lossless compression format: There must be datasets that need more memory after compression. It is up to the engineer to decide which format to use.

Things get a bit more complicated when we allow backreferences: It is often the case that a text contains repetitions. In many programming languages, for example, in the beginning, there are a lot of import or include commands. In addition to saving your bytes, you can also save a backreference, which is a pair , where is the distance, the number of bytes we have to overjump until we have the beginning of the repeated string, and is the length of the backreference. For example, let's say we have the string (we do not care about the actual representation of that file "on the metal", since this is a more sophisticated problem and highly depends on the underlying system). Then we could save this as . Of course, as before, we need reserved bytes to denote these backreferences, and therefore, there are situations in which this form of compression is even bad. However, in practice, this method is very useful and often gains a lot of compression. Especially, modern data formats like XML employ a lot of redundancy, which has some advantages when working with them locally, but is a waste of bandwidth when sending them, and here it can be very efficient. Of course, for every string, there exists a minimal representation with backreferences. However, it is not practical to calculate it, even for short strings, but the intuitive "linear" algorithm, just reading the string from left to right and maintaining a dictionary usually provides sufficient results.

While RLE tries to remove duplicate substrings, it is also often the case that only a small amount of actual possible bytes are used, or at least some bytes are used very seldom, compared to others. Therefore it is plausible to increase the amount of memory needed for the less frequently used bytes, and in exchange decrease the amount for the more frequently used. There are several ways to do this. The one we want to look at here is the use of Huffman codings. Firstly, we are given some alphabet. Even in practice, this alphabet needs not to fit into a byte, it may contain more than characters. So say we have an alphabet , and a sequence of characters of length . Now let be the number of times the character occurs in . As we want to save our string as sequence of bits, we have to map every character on a unique bit sequence, in a way that when reading the whole bit sequence from left to right, no ambiguousity occurs. The code must be prefix free: No sequence of one character is allowed to be the prefix of another one, that is, we can form a binary tree such that each branch is mapped to a character. If denotes the (not yet known) lengths of the huffman codes, we want to minimize the number of bits required to save our string, and this number is . The following procedure creates a tree which tries to do this:

• Step 1: Begin with the set of pairs of leaf nodes labelled with characters, and their frequency.
• Step 2: If contains only one element, return it: It is your huffman tree. If contains at least two elements, let be the two pairs with the lowest frequencies , and set , thus, replacing the two trees by a new higher tree.
• Step 3: Proceed at Step 1 with the new .

It is easy to see that if the frequencies are powers of two, this produces an optimal code.

Huffman codes are not unique, as we can "mirror" subtrees of the code. However, with some additional restrictions, we can make it unique. Shorter codes must lexicographically precede longer codes. Codes of the same length must have the same lexicographic ordering as the characters they order. And the whole coding must be lexicographically dense, and contain a string that only contains zeroes. For example, consider the huffman code . is shorter than , but does not lexicographically precede it. lexicographically precedes , however, does not precede . The corresponding canonical Huffman code, satisfying all the properties, is . It is easy to show (and left as an exercise) that each huffman code can be canonicalized.

So I was thinking about the meaning of life (or actually, about the discussions about the meaning of life I have heard), and found a nice duality to logic.

The problem with the meaning of life is that you want to have an entity that implies that life actually makes sense. The German phrase "Sinn des Lebens" focuses even more on this, as "Sinn" can be translated to "meaning", but also to "use" and "sense". It is often said that the meaning of life is to make the world a better place for living. If this does the job for you, then accept it, but one might ask what the meaning of the world is at all - which is as hard to answer as the original question. It is also often said that the meaning of life is to serve some deity, be it personal or pantheistic. But then you might question what the meaning of this deity's existence is and question is mostly disregarded, or even prohibited. A dogma - an "axiom" - is introduced that defines an entity that has a meaning, and questioning it is basically not allowed. Just "enjoying life" is another pragmatic way to deal with this problem, and is even more direct: Just ignore the problem.

However, let us look closer at the actual problem. Say we have our life, call it . We ask for some entity that implies that actually makes sense. And then we might question this new entity and get and so on, so we get an infinite ascending chain of entities that imply that the entities below make sense. And then we can define an entity that ensures that all the infinitely many entities we already defined make sense. And since is the smallest ordinal number that is infinite, we call it . And of course, we can define , and so on. In fact, for every ordinal number , we can define . However, itself is a proper class: We cannot talk about it inside our system. We can assume its existence, because we can assume that the stuff we cannot talk about anymore behaves similar to the stuff we can talk about. We talk about "something that is bigger than everything we can talk about", but this does not make sense anymore: As we can talk about it, it is not bigger than everything we can talk about.

Seeking for the meaning of life is now a lot like seeking for : It is desirable, but not possible. Every system we can come up to is either inconsistent, or limited. We can postulate principles which increase the range of numbers we can talk about, like assuming that O# exists. Still, the original problem remains.

However, this just means that We cannot talk about the meaning of life without creating inconsistencies. Whether or not a meaning of life "exists" is a more complicated question, because at the latest when reaching that meta-level, it is a valid question what "existing" actually means.