Tue, 13 Mar 2012 13:30:00 GMT
Be sure to read the former parts 1, 2, 3, 4 and especially part 5 about orderings, before you read this part.
There are a lot of people trying to tell about what mathematics or a more specific topic is actually about - and they are often right in some sense, looking at it from a certain perspective. However, mostly those perspectives are missing something. Therefore, I will not make the claim that talking about infinitary objects is talking about orderings. However, what I can say is that ordering relations play an important role.
For example, many important definitions on can be made in terms of the default ordering
can be made in terms of the default ordering  , like convergence and openness.
, like convergence and openness.




There are a lot of people trying to tell about what mathematics or a more specific topic is actually about - and they are often right in some sense, looking at it from a certain perspective. However, mostly those perspectives are missing something. Therefore, I will not make the claim that talking about infinitary objects is talking about orderings. However, what I can say is that ordering relations play an important role.
For example, many important definitions on
However, there is one sort of ordering relations which especially suits the purpose of describing connections between infinitary objects: the well-orderings. We will introduce this concept here.
In part 1, we gave axioms for natural numbers. These were
- Every number has a unique successor
- Every number except
has a predecessor
- Every non-empty set has a smallest element
We now want to generalize these. To generalize something, the axioms must be loosened. Loosening the first axiom would lead to a structures mathematicians would call trees (yes, like the plant), but we do not want to discuss these here - we keep the axiom of unique successors. We have seen that the third axiom is useful in proofs. The property is called well-foundedness. We will also keep this one. So the only thing we can loosen is the second: We will allow additional elements which have no predecessor.
Now consider the set  of pairs of natural numbers. We give an ordering
of pairs of natural numbers. We give an ordering  by
by
That is, we first sort by the left element, and then, if the left elements are equal, by the right element. This is called the lexicographical order on  . It is, in fact, an ordering (exercise).
. It is, in fact, an ordering (exercise).
This relation satisfies our two remaining axioms: The unique successor of a pair  is obviously
is obviously  . To get the minimum of a set
. To get the minimum of a set  , we first notice that
, we first notice that  has a minimal element
has a minimal element  , as it is a subset of
, as it is a subset of  , and then
, and then  also has a smallest element
also has a smallest element  , and then,
, and then,  is a minimal element of
is a minimal element of  . The "zero" of this ordering, that is, the smallest element, is obviously
. The "zero" of this ordering, that is, the smallest element, is obviously  .
.
A further example for a pair with no predecessor is  . Even though there are infinitely many pairs, namely
. Even though there are infinitely many pairs, namely  smaller than
smaller than  , none of them is the predecessor of
, none of them is the predecessor of  .
.
Now, keep in mind that we still want a generalization of the order of the natural numbers. We can embed  into
into  using the injective homomorphism
using the injective homomorphism  . As mathematicians are lazy, we will now just identify the naturals by this homomorphism, that is, we will actually write
. As mathematicians are lazy, we will now just identify the naturals by this homomorphism, that is, we will actually write  instead of
instead of  . With this inclusion,
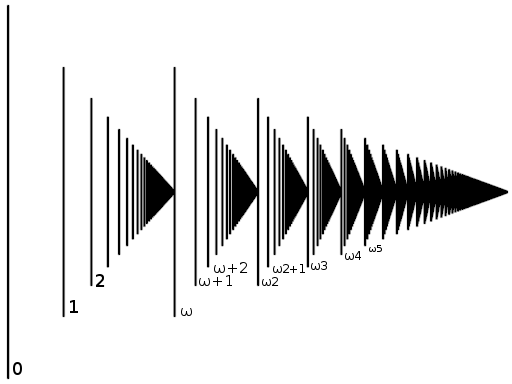
. With this inclusion,  becomes the first element that is larger than all the "naturals". We will - for now - write
becomes the first element that is larger than all the "naturals". We will - for now - write  for
for  , and
, and  for
for  , and - to make it even more confusing -
, and - to make it even more confusing -  for
for  .
.
In fact, we can then do addition with these new objects, and multiplication with a new object and a natural, as we did with naturals - with distributive and associative laws:
However, what we cannot do yet is multiplying two of these new objects:  is not defined yet. We can generalize the above concept by looking at infinite sequences of natural numbers, which end in a sequence of zeroes, that is,
is not defined yet. We can generalize the above concept by looking at infinite sequences of natural numbers, which end in a sequence of zeroes, that is,  ,
,  , etc., and apply the lexicographical order on their reversed sequences:
, etc., and apply the lexicographical order on their reversed sequences:
That is, we get for the largest index  such that
such that  , and use its order. Our former ordering of pairs can be embedded by
, and use its order. Our former ordering of pairs can be embedded by  .
.
Now,  , and
, and  , and generally,
, and generally,  , and we can write a sequence
, and we can write a sequence  as
as  . This definition is only provisional: the actual definition is more complicated, especially, addition is not commutative,
. This definition is only provisional: the actual definition is more complicated, especially, addition is not commutative,  . Our definition works well if we always have larger numbers on the left side of the addition, and we will silently ignore the fact that we did not define it for other cases.
. Our definition works well if we always have larger numbers on the left side of the addition, and we will silently ignore the fact that we did not define it for other cases.
Ordering relations like  are called well-orderings: A well-ordering
are called well-orderings: A well-ordering  on a set
on a set  is an ordering, for which every subset
is an ordering, for which every subset  has a smallest element.
has a smallest element.
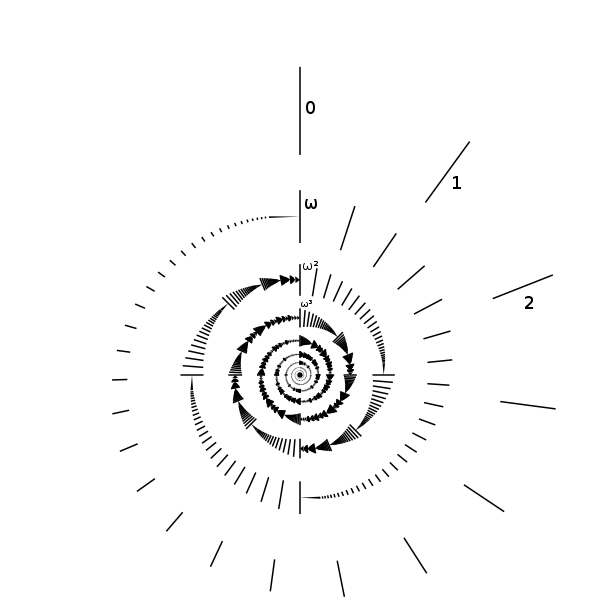
As you have seen in the examples, with well-orderings we can get beyond the tower of natural numbers, into "transfinite" numbers. However, well-orderings have a surprising property, which makes them suitable for analysis of infinity:
Let  be a well-ordering, and
be a well-ordering, and  be a strictly decreasing sequence of elements of
be a strictly decreasing sequence of elements of  . Then
. Then  is of finite length.
is of finite length.
Proof: The set of sequence elements  must have a smallest element. As
must have a smallest element. As  is strictly decreasing, after reaching this element,
is strictly decreasing, after reaching this element,  must end immediately.
must end immediately.
Interestingly, we can now find an ordering relation on well-orderings: Let  and
and  be well-orderings, then there is either an injective homomorphism
be well-orderings, then there is either an injective homomorphism  or an injective homomorphism
or an injective homomorphism  or both, when they are isomorphic - as this is a bit harder to prove, we omit the proof.
or both, when they are isomorphic - as this is a bit harder to prove, we omit the proof.
So we can find a relation  between well-orderings, where
between well-orderings, where  shall mean that there exisit an injective homomorphism
shall mean that there exisit an injective homomorphism  . If we have
. If we have  and
and  , then the well-ordernigs are isomorphic, we write
, then the well-ordernigs are isomorphic, we write  for that.
for that.
The collection  contains all the well-orderings isomorphic to a well-ordering
contains all the well-orderings isomorphic to a well-ordering  , and as it contains all the relevant structural information of the ordering, it is called the ordering type of
, and as it contains all the relevant structural information of the ordering, it is called the ordering type of  .
.
And now ... it gets complicated. We defined  as a collection, but not as a set! The axioms of set theory require sets to obey some restrictions - and this collection does not do so. It is a so-called proper class, that is a collection which is too big to be a set. However, it is not necessary to understand the reasons right now, and so I will not give any. The important thing is that being proper classes makes ordering types pretty hard to handle, which is why mathematicians had to invent a different method. For every ordering type, they gave a representative, that is a well-ordering which is isomorphic to the others, but has an additional property that uniquely determines it. These representatives are called ordinal numbers.
as a collection, but not as a set! The axioms of set theory require sets to obey some restrictions - and this collection does not do so. It is a so-called proper class, that is a collection which is too big to be a set. However, it is not necessary to understand the reasons right now, and so I will not give any. The important thing is that being proper classes makes ordering types pretty hard to handle, which is why mathematicians had to invent a different method. For every ordering type, they gave a representative, that is a well-ordering which is isomorphic to the others, but has an additional property that uniquely determines it. These representatives are called ordinal numbers.
While originally I wanted to discuss ordinal numbers in detail with this post, the post turns out to become longer than I expected. I think, for this time, the amount of new knowledge floating through my dear readers' brains is enough.
Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)