Sat, 28 Jan 2012 18:53:37 GMT
Via The Old New Thing, I found this video about a "fault tolerant heap" in Windows 7. They analyzed a lot of program bugs, and found a relevant part of them being heap corruptions. As a temporary solution for the most common of these, they created a mode for running applications which uses techniques to prevent the most common of them.
On the one hand, this sounds like a very bad hack, which - from my purist point of view - should not be used at all. But on the other hand, it is a technical accomplishment. So, the criticism here does not go against the engineers from Microsoft. They probably have to face stupid programmers and stupid users every day, and just try to find ways of handling them more efficiently.
However, I consider this approach dangerous, in the sense that programmers may tend to just specify to "turn on the fault tolerant heap" (and let their setup do this) rather than programming cleanly. I can imagine this being a lot easier in many cases - and time is money. And then, in ten years, when a lot of new stupid "standard" software uses it, this will not be a feature anymore, but rather a necessity for the software to run.
I cannot really understand why this kind of bug is still an issue, anyway. There are good, fast and stable implementations of automatic memory managers out there, especially garbage collectors, which should be sufficient for most of the software (which is bloated anyway, so nobody will notice the difference). Even for macro assemblers like C++, if you want it desperately.
I mean, there are a lot of remaining bugs which cannot be prevented that way, but that kind of bug is a solved problem. And programmers can concentrate on other stuff, and will probably be more productive when not having to think about memory management.
On the one hand, this sounds like a very bad hack, which - from my purist point of view - should not be used at all. But on the other hand, it is a technical accomplishment. So, the criticism here does not go against the engineers from Microsoft. They probably have to face stupid programmers and stupid users every day, and just try to find ways of handling them more efficiently.
However, I consider this approach dangerous, in the sense that programmers may tend to just specify to "turn on the fault tolerant heap" (and let their setup do this) rather than programming cleanly. I can imagine this being a lot easier in many cases - and time is money. And then, in ten years, when a lot of new stupid "standard" software uses it, this will not be a feature anymore, but rather a necessity for the software to run.
I cannot really understand why this kind of bug is still an issue, anyway. There are good, fast and stable implementations of automatic memory managers out there, especially garbage collectors, which should be sufficient for most of the software (which is bloated anyway, so nobody will notice the difference). Even for macro assemblers like C++, if you want it desperately.
I mean, there are a lot of remaining bugs which cannot be prevented that way, but that kind of bug is a solved problem. And programmers can concentrate on other stuff, and will probably be more productive when not having to think about memory management.
Show comments (Requires JavaScript, loads external content and cookies from Disqus.com)
Mon, 23 Jan 2012 13:00:00 GMT
Before I start, I clearly have to say that almost all websites suck! Especially official websites, like websites of universities or government agencies, on such websites, you mostly find everything except what you are searching for.
So why is the title of this post then about British websites? Well, I recently had to deal with some of them, for applications for vacancies. They all require cookies and JavaScript - Cookies are understandable somehow, but JS is not! And for cookies, simple session cookies should be sufficient, and they should not be public. Some of the sites even have stuff by Google - I really do not want this (usually) on a university website.
But the worst part of all is when there are .doc-files. Why the hell would anybody want a .doc file on a website? Many .doc files can be viewed using LibreOffice, but mostly there are several problems with the actual design.
On some recent sites, such .doc files have been used as "forms" one should fill out and then send back per e-mail. Which is extremely annoying. Not everybody has MS Word, MS Word is pretty expensive, and not even everybody uses Windows or Mac OS X. And OpenOffice sometimes makes mistakes. So: Just do not use .doc files!
And in any case: Do not rely on your form being applicable to everybody. Have somebody to answer e-mails when there is a problem with filling the form. One example why is given here.
You might argue that it is easy to say what is wrong, but hard to say what is right. So, here are several suggestions on how to (probably) do it right. Of course, without any warrianty.
Firstly, of course, one should discuss what exactly "right" means. The first thing is, of course, that the software to fill in the forms must be free of charge, and available on all - well, at least the mainly used (including Linux!) - systems, so everyone can use it. Ideally, there must be an open source software product. But of course, it is useless to try to make something run on all systems - there are so much screwed up configurations out there, that this is clearly impossible. The obvious solution: let a human control it. There is no need to do much, just checking whether everything in some filled form is right, and if not, sending a mail requesting the missing information, should be sufficient. But please, let somebody who "knows about computers" do that! The least helpfull thing is a secretary, asking you why you "not just open it with Word".
One alternative for filling forms is the pdf form format. It works with many programs, also open source software. The problem is that it is not widespread yet, and ... sucks ... somehow.
Similarly, there are Google Docs. The main disadvantage is: Google knows what you write. But ... who cares?
A possibility similar to pdf forms are pdf files which can be changed with software like Okular, Xournal, or by just printing, filling and scanning them. The main disadvantage is that probably most people are too stupid to use them. They do not have a scanner (and do not know that most copy shops have one), they do not know how to properly print pdf files (!!), let alone annotating them.
Alternatively, png images can be changed using MS Paint, Gimp, etc.
Also widespread is the support of Flash and Java applets. Why ever one would need Flash or Java for filling a simple form, this should be something everybody can use. Of course, both base on closed source technologies, but both have open source alternatives with which one could try to stay compatible with. Explicitly stating and maintaining this compatibility would of course be necessary. An advantage of Java applets is that this is a comparably old technology, so it is comparably stable.
And now ... I come to the "revolutionary" part, which some webdesigners would kill me for even thinking about: Using old technology that is widespread und has proven stable!
For example, it may not look as good as a well-designed Word document with a nice shiny header, but still, a simple text document (.txt) which is designed to be viewed using a monospace font, should be sufficient for most purposes. The advantage is that vitally every system can show them. One problem, however, is the encoding. You can request the user to use UTF-8, but many users do not know what that means. Requesting the users not to use special characters is hard, when for example his name contains them. Good editors like Emacs and VI allow annotations that indicate the encoding. Notepad supports BOMs. It may not be perfect, but it should work in many cases. A major disadvantage is that every user can freely screw up the form. But this can be done with .doc files as well.
Finally, there is one technology which is widespread, takes care of encoding, and can be viewed by vitally every device: Good old web forms and HTTP. The main disadvantage is that you cannot just pass a file to the user, which he then mails you, but you have to provide some server application. However, this is normally not an issue. Creating some CSV-Output, such that the user can proceed working with the form later, when uploading it again, as well as creating a beautiful PDF from its input to mail to some secretary, can both be considered as solved problems. And - surprise - you do not need any JavaScript for this.
So why is the title of this post then about British websites? Well, I recently had to deal with some of them, for applications for vacancies. They all require cookies and JavaScript - Cookies are understandable somehow, but JS is not! And for cookies, simple session cookies should be sufficient, and they should not be public. Some of the sites even have stuff by Google - I really do not want this (usually) on a university website.
But the worst part of all is when there are .doc-files. Why the hell would anybody want a .doc file on a website? Many .doc files can be viewed using LibreOffice, but mostly there are several problems with the actual design.
On some recent sites, such .doc files have been used as "forms" one should fill out and then send back per e-mail. Which is extremely annoying. Not everybody has MS Word, MS Word is pretty expensive, and not even everybody uses Windows or Mac OS X. And OpenOffice sometimes makes mistakes. So: Just do not use .doc files!
And in any case: Do not rely on your form being applicable to everybody. Have somebody to answer e-mails when there is a problem with filling the form. One example why is given here.
You might argue that it is easy to say what is wrong, but hard to say what is right. So, here are several suggestions on how to (probably) do it right. Of course, without any warrianty.
Firstly, of course, one should discuss what exactly "right" means. The first thing is, of course, that the software to fill in the forms must be free of charge, and available on all - well, at least the mainly used (including Linux!) - systems, so everyone can use it. Ideally, there must be an open source software product. But of course, it is useless to try to make something run on all systems - there are so much screwed up configurations out there, that this is clearly impossible. The obvious solution: let a human control it. There is no need to do much, just checking whether everything in some filled form is right, and if not, sending a mail requesting the missing information, should be sufficient. But please, let somebody who "knows about computers" do that! The least helpfull thing is a secretary, asking you why you "not just open it with Word".
One alternative for filling forms is the pdf form format. It works with many programs, also open source software. The problem is that it is not widespread yet, and ... sucks ... somehow.
Similarly, there are Google Docs. The main disadvantage is: Google knows what you write. But ... who cares?
A possibility similar to pdf forms are pdf files which can be changed with software like Okular, Xournal, or by just printing, filling and scanning them. The main disadvantage is that probably most people are too stupid to use them. They do not have a scanner (and do not know that most copy shops have one), they do not know how to properly print pdf files (!!), let alone annotating them.
Alternatively, png images can be changed using MS Paint, Gimp, etc.
Also widespread is the support of Flash and Java applets. Why ever one would need Flash or Java for filling a simple form, this should be something everybody can use. Of course, both base on closed source technologies, but both have open source alternatives with which one could try to stay compatible with. Explicitly stating and maintaining this compatibility would of course be necessary. An advantage of Java applets is that this is a comparably old technology, so it is comparably stable.
And now ... I come to the "revolutionary" part, which some webdesigners would kill me for even thinking about: Using old technology that is widespread und has proven stable!
For example, it may not look as good as a well-designed Word document with a nice shiny header, but still, a simple text document (.txt) which is designed to be viewed using a monospace font, should be sufficient for most purposes. The advantage is that vitally every system can show them. One problem, however, is the encoding. You can request the user to use UTF-8, but many users do not know what that means. Requesting the users not to use special characters is hard, when for example his name contains them. Good editors like Emacs and VI allow annotations that indicate the encoding. Notepad supports BOMs. It may not be perfect, but it should work in many cases. A major disadvantage is that every user can freely screw up the form. But this can be done with .doc files as well.
Finally, there is one technology which is widespread, takes care of encoding, and can be viewed by vitally every device: Good old web forms and HTTP. The main disadvantage is that you cannot just pass a file to the user, which he then mails you, but you have to provide some server application. However, this is normally not an issue. Creating some CSV-Output, such that the user can proceed working with the form later, when uploading it again, as well as creating a beautiful PDF from its input to mail to some secretary, can both be considered as solved problems. And - surprise - you do not need any JavaScript for this.
Tue, 17 Jan 2012 20:15:00 GMT
We have seen a basic introduction to infinity and its definition in part 1 of this series, and in part 2, we have seen that infinitary processes might have a finite outcome. In part 3, we have seen a lot of nice examples getting deeper into the topic of infinite curves and planes. However, we moved away from the actual question about how many elements a set has, as the curves are more demonstrative in the beginning. With this post, we want to turn back to this question again.
Let us recall how we defined infinity in part 1: A set is infinite if and only if there is a bijection into a proper subset.
While it is pretty clear that there are multiple finite sets with different numbers of elements, the question whether there are infinite sets that contain more elements than has not been answered yet. And while it is pretty clear that for two finite sets, we can always say which of them is greater, this is not clear when talking about infinite sets. The definition is pretty obvious: If there is a bijection from a set
has not been answered yet. And while it is pretty clear that for two finite sets, we can always say which of them is greater, this is not clear when talking about infinite sets. The definition is pretty obvious: If there is a bijection from a set  into a subset of
into a subset of  , then
, then  has more or equally many elements as
has more or equally many elements as  , we will denote this by
, we will denote this by  .
.
So as said, the first question which arises is, whether two sets are always comparable. This follows directly from the well-ordering theorem, but we will not discuss this proof here, since it is sophisticated. We just keep in mind that for any two sets and
and  , we have
, we have  or
or  .
.
Let us denote by that the sets
that the sets  and
and  contain equally many elements, that is, there is a bijection between them. Then the obvious question is whether
contain equally many elements, that is, there is a bijection between them. Then the obvious question is whether  and
and  implies
implies  . Do not let yourself confuse by the notation: This is not clear! Essentially, the question is whether when we have a bijection from
. Do not let yourself confuse by the notation: This is not clear! Essentially, the question is whether when we have a bijection from  to a subset of
to a subset of  and a bijection from
and a bijection from  into a subset of
into a subset of  , we also have a bijection between
, we also have a bijection between  and
and  .
.
By the Cantor-Bernstein-Theorem, this holds, but we will not discuss this here, and just accept that it works for all sets we will consider.
Now, when thinking about the "number" of Elements of the set of positive integers, two obvious questions arise: Whether there is an infinite set smaller than
of positive integers, two obvious questions arise: Whether there is an infinite set smaller than  , and whether there is an infinite set greater than
, and whether there is an infinite set greater than  . For the first question, it is sufficient to prove that every infinite subset of
. For the first question, it is sufficient to prove that every infinite subset of  has a bijection into
has a bijection into  . This can be done by the minimum principle defined in part 1, and is left to the interested reader. So indeed,
. This can be done by the minimum principle defined in part 1, and is left to the interested reader. So indeed,  is the "smallest" infinite set, in the sense that every other infinite set has at least as much elements as
is the "smallest" infinite set, in the sense that every other infinite set has at least as much elements as  .
.
In part 1, we have already seen, that the first obvious "larger" set, the set of integers, is not larger than
of integers, is not larger than  : The mapping
: The mapping
 , that is,
, that is,
 is
is  , is a
bijection. So in fact, there are as many non-negative integers, as
there are integers at all.
, is a
bijection. So in fact, there are as many non-negative integers, as
there are integers at all.
The next obvious candidate is the set of pairs
of pairs  of nonnegative integers. You can imagine them as points of a "grid":
of nonnegative integers. You can imagine them as points of a "grid":

The question can now be seen more geometrical: Is it possible, to arrange these points on a curve? And of course, it is:

We get the sequence . This sequence is defined by the Cantor-Pairing-Function
. This sequence is defined by the Cantor-Pairing-Function  . It is a bijection, and we call its inverse for the right side
. It is a bijection, and we call its inverse for the right side  and its inverse for the left side
and its inverse for the left side  , thus,
, thus,  .
.
So, is not larger than
is not larger than  . In fact, therefore, trivially, also the set of triples, quartuples, etc., of natural numbers are not larger than the set of natural numbers, as we can encode for example triples by
. In fact, therefore, trivially, also the set of triples, quartuples, etc., of natural numbers are not larger than the set of natural numbers, as we can encode for example triples by  .
.
So, the next obvious candidate would be to unite all of these sets, gaining the set of finite sequences of natural numbers. As you might expect, this set is also countable, and there is a more general theorem that states that every union of countably many countable sets is countable itself, which would hold here. But in this case, we can show it more directly, by giving a bijection. Firstly, let
of finite sequences of natural numbers. As you might expect, this set is also countable, and there is a more general theorem that states that every union of countably many countable sets is countable itself, which would hold here. But in this case, we can show it more directly, by giving a bijection. Firstly, let  be the bijection from the
be the bijection from the  -tuples into the natural numbers (where
-tuples into the natural numbers (where  ), which exists as shown above. Then define
), which exists as shown above. Then define

Its inverse is given by

As this looks rather theoretic and confusing, here is a Java-Program which actually does this (I hope):
So in fact, not even the set of finite sequences of natural numbers is larger than the set of natural numbers.
Ok, the next canonical candidate would be the set of rational numbers, . But every rational number is of the form
. But every rational number is of the form  , where
, where  and
and  are coprime, and this form is unique except for
are coprime, and this form is unique except for  . That is,
. That is,  can be regarded as a subset of
can be regarded as a subset of  , which means that it is, actually, countable.
, which means that it is, actually, countable.
Ok, the rationals are not larger than the set of natural numbers. But now, we finally approach to a set which is actually larger: The set of real numbers.
of real numbers.
In part 1 we have seen the following bijection, which makes it sufficient to show that there is no bijection![f:\mathbb{N}\rightarrow]0;1[](/latex?n=f24787ed17126814417feb1ed48183183160fe9d1d40461436cc39f3bc70f41b) , because the connection of two bijections is a bijection again, obviously.
, because the connection of two bijections is a bijection again, obviously.
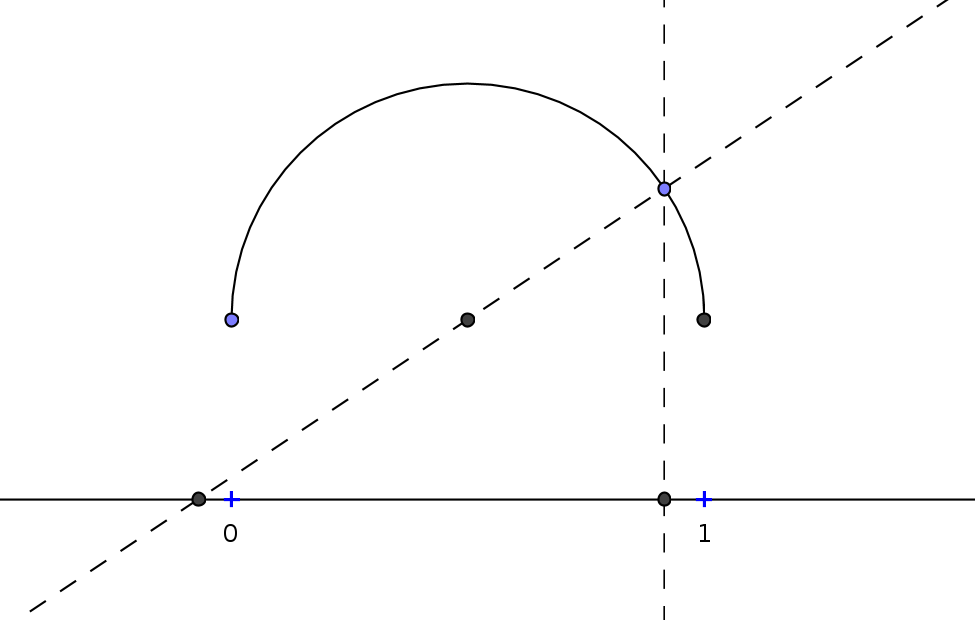
So assume there was a bijection![f:\mathbb{N}\rightarrow]0;1[](/latex?n=f24787ed17126814417feb1ed48183183160fe9d1d40461436cc39f3bc70f41b) . Every element of
. Every element of ![]0;1[](/latex?n=abcbe6aa6f94b3cb46c96e2187212549f6dc3ceba7745679326455ec65bcd4f6) has a decimal representation, say,
has a decimal representation, say,  with
with  , and we may assume that, if possible, this representation is stationary, that is, ends with infinitely many zeroes (we must assume this, since for example
, and we may assume that, if possible, this representation is stationary, that is, ends with infinitely many zeroes (we must assume this, since for example  as we have seen in part 1).
as we have seen in part 1).
Now define for all

Then there is a real number , and this real number is distinct from all
, and this real number is distinct from all  . So,
. So,  cannot be surjective. Contradiction.
cannot be surjective. Contradiction.
The same argument also proves that there is no surjective such , that is,
, that is,  contains strictly more elements. The powerset
contains strictly more elements. The powerset  , the set of subsets of
, the set of subsets of  , is another example, and the proof for this is somewhat similar: Considering a function
, is another example, and the proof for this is somewhat similar: Considering a function  , the set
, the set  is not in the range of
is not in the range of  (proof: exercise!), so
(proof: exercise!), so  cannot be surjective.
cannot be surjective.
Now of course, the question arises whether is larger or smaller than
is larger or smaller than  . They are of equal cardinality, and it is possible to give a bijection, but it is rather sophisticated, so this is left as an exercise for the interested reader.
. They are of equal cardinality, and it is possible to give a bijection, but it is rather sophisticated, so this is left as an exercise for the interested reader.
Let us recall how we defined infinity in part 1: A set is infinite if and only if there is a bijection into a proper subset.
While it is pretty clear that there are multiple finite sets with different numbers of elements, the question whether there are infinite sets that contain more elements than
So as said, the first question which arises is, whether two sets are always comparable. This follows directly from the well-ordering theorem, but we will not discuss this proof here, since it is sophisticated. We just keep in mind that for any two sets
Let us denote by
By the Cantor-Bernstein-Theorem, this holds, but we will not discuss this here, and just accept that it works for all sets we will consider.
Now, when thinking about the "number" of Elements of the set
In part 1, we have already seen, that the first obvious "larger" set, the set
The next obvious candidate is the set

The question can now be seen more geometrical: Is it possible, to arrange these points on a curve? And of course, it is:

We get the sequence
So,
So, the next obvious candidate would be to unite all of these sets, gaining the set
Its inverse is given by
As this looks rather theoretic and confusing, here is a Java-Program which actually does this (I hope):
public class CantorStuff {
public static int cantorPair (int x, int y) {
x--; y--;
return (x+y)*(x+y+1)/2+y+1;
}
public static int[] cantorPairToNumbers (int z) {
z--;
int w = (int) Math.floor((Math.sqrt(8*z+1)-1)/2);
int t = (w*w+w)/2;
int y = z-t;
return new int [] { w-y+1, y+1 };
}
public static int sequenceToNum (int[] seq) {
int ret = seq[seq.length - 1];
for (int i = seq.length - 2; i >= 0; i--) {
ret = cantorPair(seq[i], ret);
}
return cantorPair(seq.length, ret);
}
public static int[] numToSequence (int num) {
int[] ctpn = cantorPairToNumbers(num);
int[] ret = new int[ctpn[0]];
for (int i = 0; i < ret.length - 1; i++) {
ctpn = cantorPairToNumbers(ctpn[1]);
ret[i] = ctpn[0];
}
ret[ret.length - 1] = ctpn[1];
return ret;
}
public static void main (String[] args) {
if (args[0].equals("num")) {
int num = Integer.parseInt(args[1]);
int[] seq = numToSequence(num);
for (int i = 0; i < seq.length; i++) {
System.out.print(seq[i] + " ");
}
System.out.println("");
} else if (args[0].equals("seq")) {
int len = args.length - 1;
int[] seq = new int[len];
for (int i = 1; i <= len; i++) {
seq[i-1] = Integer.parseInt(args[i]);
}
System.out.println(sequenceToNum(seq));
}
}
}
So in fact, not even the set of finite sequences of natural numbers is larger than the set of natural numbers.
Ok, the next canonical candidate would be the set of rational numbers,
Ok, the rationals are not larger than the set of natural numbers. But now, we finally approach to a set which is actually larger: The set
In part 1 we have seen the following bijection, which makes it sufficient to show that there is no bijection

So assume there was a bijection
Now define for all
Then there is a real number
The same argument also proves that there is no surjective such
Now of course, the question arises whether
Thu, 12 Jan 2012 14:30:00 GMT

Mon, 02 Jan 2012 01:08:23 GMT
In a former post (on my old blog), I already had the idea of using SIGSEGV-handlers to create a crude form of lazy evaluation. However, this was not very usable yet. I meanwhile engineered around a bit, and found out a lot of interesting stuff about memory management, and signal handling in general. Though I do not think that this is a good way of doing lazy evaluation anymore, it was worth learning this much. Still, with the proper kernel support, I think lazy evaluation could be implemented easier, it is just that I do not think that SIGSEGV-handlers are the appropriate way to do this. However, keep in mind that I am not an expert, I might be wrong with what I say, and I am open to constructive comments of any kind.
Also, this post is long and I give a lot of intermediate steps until the final end, since the outcome is not as interesting as the many facts one can learn from it, I think.
So, since in the beginning, I did some assembler-haxxory, I wondered how exactly this signal handling stuff worked. If I had to create a signal handling architecture, I would probably just save the context of the program into a special reserved memory region, and then call the signal handler, leaving everything else to this handler. That is due to the fact that I think it is the best for a kernel to keep quiet as long as possible.
Linux does something else however. It maps a memory region into the process, called the vsyscall-page. It used to be on the next-to-last block in the address space, but meanwhile it is, as far as I read, on a randomized position in memory. There, the current system time is saved, and some other functions which can be called instead of calling a syscall, so this is an optimization.
Now, when a signal handler is called, it pushes a return adress on the stack, such that when the handler returns, the process jumps into this vsyscall-page. That page then calls the sigreturn-syscall (see 5.6@here). Two interesting things related to that topic: Handling signals in assembly, and the list of Linux syscalls.
So far with the theory. Let us dig in a bit deeper. One problem with the approach I had in my former post on this topic was that the actual memory page had to be allocated after the segmentation fault. It was not possible to redirect the process to some other memory region. For this, two things are necessary.
Firstly, every segmentation fault comes from some memory accessing assembler instruction, which dereferences some register. When jumping back from the handler, this instruction is called again, and causes the SIGSEGV to be sent again. We have to set the register to a new value, pointing to the place where the lazily allocated object is saved.
The register state is saved in a ucontext-structure documented in setcontext(2). It contains a non-portable mcontext-structure, which is defined in sys/ucontext.h. It is not even portable across x86_32 and x86_64. It has an array gregs[], in which the register values are saved, and from which they are restored. If we know the dereferenced register, we can therefore set it to something else. With a bit assembler magic, we can therefore already get the following code:
The output of this program is "42". And even though the program segfaults, it does not occur in dmesg.
However, we do not want assembly code, if possible. That is, we do not want to assume, that it is the ECX-Register which was dereferenced, but we need to know which register was. Therefore, we use a library for x86 disassembly: libudis86. We just disassemble the code at the instruction pointer in our gregs[]-array, and see what it does. Here is the code we get:
With this, we can lazily evaluate one object.
Secondly, we need every memory access to be dereferenced twice, so we need a local pool of addresses - so we can do it for more than one object.
We will use Matthias Benkard's implementation of Patricia Trees to achieve a dynamic array from protected pointers to actual functions. We also need a slice allocator. Actually, creating that code was rather sophisticated, and I do not want to post anything as "finished" yet, if you are interested in this most general code, look at my git repository for this project. It defines a function for creating list comprehensions from a function from integers to integers, which may depend on the actual list.
However, that code is not threadsafe. Making it more threadsafe is one of my aims with this project, if I keep working at it.
Having this work so far, of course I do not think that this is a good solution. Segmentation faults are faults, by design, and they should be considered faults. That does not mean that they should not be handled properly (which most software does not do), but they should not be produced on purpose. Rather, the kernel should add another state of memory pages, say "lazy pages", which may be allocated, but on which also a signal is sent, or some other sort of interrupt.
Some other sort of interrupt would be better, since signal handling involves two context switches. In fact, it would be sufficient to just push the state of the thread on the stack, and jump to a handling function, without having to call sigreturn. Handling such an interrupt does not involve anything on the background of the process, so the state can be restored by the handling function itself, at least mostly. Maybe a flag, indicating whether some sort of sigreturn is to be called, could be helpful, for example, if the kernel had to extend the stack or something similar.
Also, this post is long and I give a lot of intermediate steps until the final end, since the outcome is not as interesting as the many facts one can learn from it, I think.
So, since in the beginning, I did some assembler-haxxory, I wondered how exactly this signal handling stuff worked. If I had to create a signal handling architecture, I would probably just save the context of the program into a special reserved memory region, and then call the signal handler, leaving everything else to this handler. That is due to the fact that I think it is the best for a kernel to keep quiet as long as possible.
Linux does something else however. It maps a memory region into the process, called the vsyscall-page. It used to be on the next-to-last block in the address space, but meanwhile it is, as far as I read, on a randomized position in memory. There, the current system time is saved, and some other functions which can be called instead of calling a syscall, so this is an optimization.
Now, when a signal handler is called, it pushes a return adress on the stack, such that when the handler returns, the process jumps into this vsyscall-page. That page then calls the sigreturn-syscall (see 5.6@here). Two interesting things related to that topic: Handling signals in assembly, and the list of Linux syscalls.
So far with the theory. Let us dig in a bit deeper. One problem with the approach I had in my former post on this topic was that the actual memory page had to be allocated after the segmentation fault. It was not possible to redirect the process to some other memory region. For this, two things are necessary.
Firstly, every segmentation fault comes from some memory accessing assembler instruction, which dereferences some register. When jumping back from the handler, this instruction is called again, and causes the SIGSEGV to be sent again. We have to set the register to a new value, pointing to the place where the lazily allocated object is saved.
The register state is saved in a ucontext-structure documented in setcontext(2). It contains a non-portable mcontext-structure, which is defined in sys/ucontext.h. It is not even portable across x86_32 and x86_64. It has an array gregs[], in which the register values are saved, and from which they are restored. If we know the dereferenced register, we can therefore set it to something else. With a bit assembler magic, we can therefore already get the following code:
#include <stdio.h>
#include <signal.h>
#include <string.h>
#include <stdlib.h>
#define __USE_GNU
#include <ucontext.h>
// set this to REG_ECX on x86_32
#define myREG REG_RCX
int k = 42;
void handle_segv(int segv, siginfo_t* siginfo, void* ucontext) {
ucontext_t* uc = (ucontext_t*) ucontext;
uc->uc_mcontext.gregs[myREG] = (greg_t) &k;
}
void cause_segv (void* ptr) {
int d;
// d = *ptr;
asm ("movl (%%ecx), %%edx" : "=d"(d) : "c"(ptr));
printf("%d\n", d);
}
int main (void) {
struct sigaction q;
bzero(&q, sizeof(q));
q.sa_sigaction = handle_segv;
q.sa_flags = SA_SIGINFO;
sigaction(11, &q, NULL);
cause_segv(NULL);
}The output of this program is "42". And even though the program segfaults, it does not occur in dmesg.
However, we do not want assembly code, if possible. That is, we do not want to assume, that it is the ECX-Register which was dereferenced, but we need to know which register was. Therefore, we use a library for x86 disassembly: libudis86. We just disassemble the code at the instruction pointer in our gregs[]-array, and see what it does. Here is the code we get:
#include <stdio.h>
#include <signal.h>
#include <string.h>
#include <stdlib.h>
#define __USE_GNU
#include <ucontext.h>
#include <udis86.h>
/* This code is only for x86_64 */
int k = 42;
void handle_segv(int segv, siginfo_t* siginfo, void* ucontext) {
ucontext_t* uc = (ucontext_t*) ucontext;
/* do disassembly at from IP */
ud_t ud_obj;
ud_init(&ud_obj);
ud_set_mode(&ud_obj, 64);
ud_set_syntax(&ud_obj, UD_SYN_ATT);
ud_set_input_buffer(&ud_obj, (unsigned char*) uc->uc_mcontext.gregs[REG_RIP],
10);
/* was disassembly successful? */
if (!ud_disassemble(&ud_obj)) {
printf("Disassembly fail!\n");
exit(-1);
}
/* is disassembly a memory-operation? */
struct ud_operand op0 = ud_obj.operand[0];
struct ud_operand op1 = ud_obj.operand[1];
struct ud_operand op;
if (op0.type == UD_OP_MEM) {
op = op0;
} else if (op1.type == UD_OP_MEM) {
op = op1;
} else {
printf("Instruction unknown\n");
exit(-1);
}
/* find out the register - this part is clumsy as we have two sets
of constants */
int setreg;
switch (op.base) {
case UD_R_RAX:
case UD_R_EAX:
setreg = REG_RAX;
break;
case UD_R_RCX:
case UD_R_ECX:
setreg = REG_RCX;
break;
case UD_R_RDX:
case UD_R_EDX:
setreg = REG_RDX;
break;
case UD_R_RBX:
case UD_R_EBX:
setreg = REG_RBX;
break;
case UD_R_RSP:
case UD_R_ESP:
setreg = REG_RSP;
break;
case UD_R_RBP:
case UD_R_EBP:
setreg = REG_RBP;
break;
case UD_R_RSI:
case UD_R_ESI:
setreg = REG_RSI;
break;
case UD_R_RDI:
case UD_R_EDI:
setreg = REG_RDI;
break;
case UD_R_R8:
case UD_R_R8D:
setreg = REG_R8;
break;
case UD_R_R9:
case UD_R_R9D:
setreg = REG_R9;
break;
case UD_R_R10:
case UD_R_R10D:
setreg = REG_R10;
break;
case UD_R_R11:
case UD_R_R11D:
setreg = REG_R11;
break;
case UD_R_R12:
case UD_R_R12D:
setreg = REG_R12;
break;
case UD_R_R13:
case UD_R_R13D:
setreg = REG_R13;
break;
case UD_R_R14:
case UD_R_R14D:
setreg = REG_R14;
break;
case UD_R_R15:
case UD_R_R15D:
setreg = REG_R15;
break;
default:
printf("Register not supported!\n");
exit(-1);
}
/* set the register - as before */
uc->uc_mcontext.gregs[setreg] = (greg_t) &k;
}
void cause_segv (int* ptr) {
int d;
d = *ptr;
printf("%d\n", d);
}
int main (void) {
struct sigaction q;
bzero(&q, sizeof(q));
q.sa_sigaction = handle_segv;
q.sa_flags = SA_SIGINFO;
sigaction(11, &q, NULL);
cause_segv(NULL);
}
With this, we can lazily evaluate one object.
Secondly, we need every memory access to be dereferenced twice, so we need a local pool of addresses - so we can do it for more than one object.
We will use Matthias Benkard's implementation of Patricia Trees to achieve a dynamic array from protected pointers to actual functions. We also need a slice allocator. Actually, creating that code was rather sophisticated, and I do not want to post anything as "finished" yet, if you are interested in this most general code, look at my git repository for this project. It defines a function for creating list comprehensions from a function from integers to integers, which may depend on the actual list.
However, that code is not threadsafe. Making it more threadsafe is one of my aims with this project, if I keep working at it.
Having this work so far, of course I do not think that this is a good solution. Segmentation faults are faults, by design, and they should be considered faults. That does not mean that they should not be handled properly (which most software does not do), but they should not be produced on purpose. Rather, the kernel should add another state of memory pages, say "lazy pages", which may be allocated, but on which also a signal is sent, or some other sort of interrupt.
Some other sort of interrupt would be better, since signal handling involves two context switches. In fact, it would be sufficient to just push the state of the thread on the stack, and jump to a handling function, without having to call sigreturn. Handling such an interrupt does not involve anything on the background of the process, so the state can be restored by the handling function itself, at least mostly. Maybe a flag, indicating whether some sort of sigreturn is to be called, could be helpful, for example, if the kernel had to extend the stack or something similar.
Tue, 27 Dec 2011 22:00:00 GMT
This is part 3 of my series on infinity.
In part 2 we have seen that there are infinitary processes with a finite outcome. In this part, we will see something, which can at least "philosophically" be considered as the other way around: How to embed infinity into finite objects.
In the end of part 1, we have already seen the following bijection:

It embeds the whole real line into a finite open interval, so reasonings about the real line become reasonings about this interval, and reasonings about this interval become reasonings about the whole real line. However, this is a bijection, mapping something of infinite length onto something of finite length, but it is not directly something we intuitively consider as an "embedding", and we might ask the question whether it is possible for a finite object to contain a line of infinite length, for example. Now consider the following construction: You start with a square (of side length 1). You cut this square into two halfs, and into the left half, you put an isosceles triangle of height 1 and width 0.5. You cut the other half again into two halfs, and put an isosceles triangle of height 1 and width 0.25 into the left one. Proceed this infinitely often, cutting the right rectangle into two halfs, and embedding an isosceles triangle into the left one. The following graphic shows this:
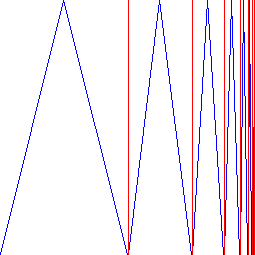
The length of the isosceles lines (blue in the graphic) of the -th triangle have length
-th triangle have length  (which follows by one of Pythagoras' theorems), but the important fact is that it is always strictly greater than
(which follows by one of Pythagoras' theorems), but the important fact is that it is always strictly greater than  , since the height is already
, since the height is already  , and each of the two lines must trivially be longer. All of the isosceles lines together form a line, the line colored blue in the graphic, and this line must be of infinite length. So in fact, it is possible for a square to contain an infinite line.
, and each of the two lines must trivially be longer. All of the isosceles lines together form a line, the line colored blue in the graphic, and this line must be of infinite length. So in fact, it is possible for a square to contain an infinite line.
Here, the special character of lines must be taken to account: Lines have no width. Lines are ideal objects, which only have a length, but do not have a width. Of course, every line we draw is not ideal, in the sense that - to be able to see it - it needs to have a width. Every line which is actually drawn is only an approximation of lines. Still, the ideal object "line" is not useless: It is a formal object which can be approximated with (probably) arbitrary precision, and its definition was a success and is implicitly used in huge parts of science.
Let us consider another graphic: Assume you draw a square of side length 1. Then centrized into this square, you draw a square of side length 0.5, and inside this, you draw a further square of side length 0.25, and so on. The following graphic shows this:

The circumference of the -th square has length
-th square has length  . So the sum of the lengths is a geometric series, as we saw in Part 2, and we have
. So the sum of the lengths is a geometric series, as we saw in Part 2, and we have  , that is, all the lines we have drawn together are of length
, that is, all the lines we have drawn together are of length  . So, informally speaking, we can draw this "with a pen": We will not need an infinite amount of color to draw it, even though it has infinitely many parts.
. So, informally speaking, we can draw this "with a pen": We will not need an infinite amount of color to draw it, even though it has infinitely many parts.
So far for this time. We have seen some nice examples of the interplay between finity and infinity, when talking about lengt. Next time it gets a bit harder, we will again look at the countability of sets.
In part 2 we have seen that there are infinitary processes with a finite outcome. In this part, we will see something, which can at least "philosophically" be considered as the other way around: How to embed infinity into finite objects.
In the end of part 1, we have already seen the following bijection:


The length of the isosceles lines (blue in the graphic) of the
Here, the special character of lines must be taken to account: Lines have no width. Lines are ideal objects, which only have a length, but do not have a width. Of course, every line we draw is not ideal, in the sense that - to be able to see it - it needs to have a width. Every line which is actually drawn is only an approximation of lines. Still, the ideal object "line" is not useless: It is a formal object which can be approximated with (probably) arbitrary precision, and its definition was a success and is implicitly used in huge parts of science.
Let us consider another graphic: Assume you draw a square of side length 1. Then centrized into this square, you draw a square of side length 0.5, and inside this, you draw a further square of side length 0.25, and so on. The following graphic shows this:

The circumference of the
So far for this time. We have seen some nice examples of the interplay between finity and infinity, when talking about lengt. Next time it gets a bit harder, we will again look at the countability of sets.
Mon, 26 Dec 2011 22:39:00 GMT

Sun, 25 Dec 2011 23:30:00 GMT
This is the second post of my series on infinity, be sure to read the first one.
We start this chapter with a nice story, "Achilles and the Tortoise", one of Zeno's Paradoxes, though we slightly adapt it. So, Achilles races against a tortoise. He gives the tortoise a 1 mile head start. Assuming Achilles is four times as fast as the tortoise, when he arrives 1 mile, the tortoise is at 1.25 miles. When he arrives 1.25, the tortoise is at 1.3125 miles. When he arrives at 1.3125, the tortoise is at 1.328125. And so on. Whenever Achilles reaches the point the tortoise was when he started, the tortoise already went further. This way, Achilles would have to go through infinitely many points, before reaching the tortoise.
Of course, this is not really a paradoxon. The problem lies in the fact that we have an infinitary process in here. As mathematicians do, we write the problem down more formally. Let be the
be the  -th point where Achilles stands, and
-th point where Achilles stands, and  the point where the tortoise stands. We have
the point where the tortoise stands. We have  and
and  , respectively. By definition, we have
, respectively. By definition, we have  , because Achilles always reaches the former point of the turtle. As the turtle has a 1 mile head start, and has
, because Achilles always reaches the former point of the turtle. As the turtle has a 1 mile head start, and has  times of Achilles' speed, we set
times of Achilles' speed, we set  , which is
, which is  . It is easy to see, that
. It is easy to see, that  , that is,
, that is,  , which is a shorter mathematical notation for such sums.
, which is a shorter mathematical notation for such sums.
Using the axioms we saw in Part 1, we can prove this formally (if you are already a little confused, just skip this proof, it is not necessary for the further understanding): Assume there is an such that
such that  , then there is a smallest such
, then there is a smallest such  . Clearly,
. Clearly,  , so
, so  . Therefore, it has a predecessor
. Therefore, it has a predecessor  , for which we must have
, for which we must have  , since
, since  was minimal. But then,
was minimal. But then,  . Contradiction.
. Contradiction.
Obviously, Achilles will pass the tortoise at some point, and obviously, this point is greater than all . We want to find out more about this point where he passes the tortoise.
. We want to find out more about this point where he passes the tortoise.

The point we are looking for, is . In fact, this is provable. But it is a bit harder than the above induction. What we have here, is a so-called geometric series. As we have
. In fact, this is provable. But it is a bit harder than the above induction. What we have here, is a so-called geometric series. As we have  , we have
, we have  , that is,
, that is,  and
and  differ in the terms
differ in the terms  and
and  , and thus we have
, and thus we have





(source)
We start this chapter with a nice story, "Achilles and the Tortoise", one of Zeno's Paradoxes, though we slightly adapt it. So, Achilles races against a tortoise. He gives the tortoise a 1 mile head start. Assuming Achilles is four times as fast as the tortoise, when he arrives 1 mile, the tortoise is at 1.25 miles. When he arrives 1.25, the tortoise is at 1.3125 miles. When he arrives at 1.3125, the tortoise is at 1.328125. And so on. Whenever Achilles reaches the point the tortoise was when he started, the tortoise already went further. This way, Achilles would have to go through infinitely many points, before reaching the tortoise.
Of course, this is not really a paradoxon. The problem lies in the fact that we have an infinitary process in here. As mathematicians do, we write the problem down more formally. Let
Using the axioms we saw in Part 1, we can prove this formally (if you are already a little confused, just skip this proof, it is not necessary for the further understanding): Assume there is an
Obviously, Achilles will pass the tortoise at some point, and obviously, this point is greater than all

The point we are looking for, is
From this, we see that, the larger  gets, the smaller
gets, the smaller  gets, and therefore, for very large
gets, and therefore, for very large  ,
,  approaches
approaches  . In fact, if we did a little more preliminary work, this would be a valid mathematical proof, and mathematicians would write
. In fact, if we did a little more preliminary work, this would be a valid mathematical proof, and mathematicians would write  , where
, where  is the symbol for "infinity", and call
is the symbol for "infinity", and call  the limit of this series. As we wrote
the limit of this series. As we wrote  for the finite sum, we can also write
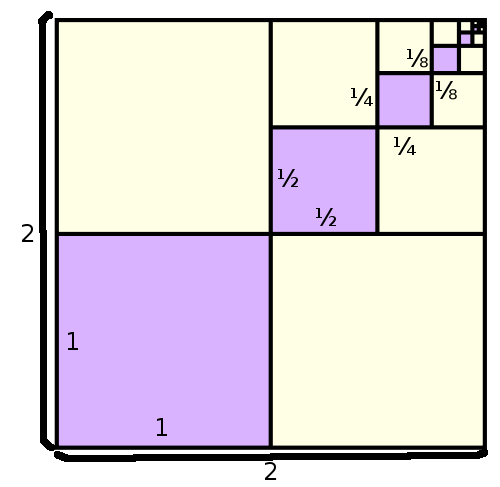
for the finite sum, we can also write  for its limit. The following graphic gives a certain geometric intuition of this fact:
for its limit. The following graphic gives a certain geometric intuition of this fact:

(source)
Of course, it is not always that easy, not every infinite process has a finite outcome. For example, obviously, the infinite sum  does not. However, we know that its finite parts get arbitrarily large, so we might say that
does not. However, we know that its finite parts get arbitrarily large, so we might say that  . This series diverges, while the above geometric series converges.
. This series diverges, while the above geometric series converges.
But even worse, consider the series  . Its finite parts are either
. Its finite parts are either  or
or  . But you cannot find any "tendency" on what happens during infinty. This series neither converges nor diverges.
. But you cannot find any "tendency" on what happens during infinty. This series neither converges nor diverges.  is not well-defined.
is not well-defined.
The above example with the tortoise was one special geometric series, the general (infinite) geometric series is  , which converges for
, which converges for  , and then has the limit
, and then has the limit  - in the case, we had
- in the case, we had  , for a general proof, consider the Wikipedia-article, or any good introduction to calculus.
, for a general proof, consider the Wikipedia-article, or any good introduction to calculus.
Even more general, we have  . With this formula, we can prove a fact quite a lot of people are not willing to understand:
. With this formula, we can prove a fact quite a lot of people are not willing to understand:  , where
, where  means the zero with infinitely many nine-digits after the decimal point. But in fact, we have
means the zero with infinitely many nine-digits after the decimal point. But in fact, we have  , which is
, which is  , which is, according to our formula,
, which is, according to our formula,  .
.
There is a general law about recurring decimal numbers you may know from school, namely,  . For example, from this follows the above,
. For example, from this follows the above,  . More precisely written, we have
. More precisely written, we have  , which follows by our above formula by
, which follows by our above formula by  .
.
As you see, studying this kind of objects can get very complicated, but produces a lot of interesting outcomes. If you did not quite get the last part, do not worry, it is rather sophisticated for a non-mathematician.
Mon, 19 Dec 2011 23:30:00 GMT
#! /bin/bash
width=22
text=0110110011011101111001011010110101110111011\
000001000010111011101100110101101011101110110011\
0101101000100011001
(
textlen=$(echo -n "$text" | wc -c)
height=$((textlen/width))
echo new $((8*width)),$((8*height))
echo fill 10,10,255,255,255
j=0; while [ "$j" -lt "$height" ]; do
i=0; while [ "$i" -lt "$width" ]; do
ftext=${text:0:1}
text=${text:1}
if [ "$ftext" "=" "0" ]; then
echo frect $((8*i)),$((8*j)),$((8*i+8)),$((8*j+8)),0,0,0;
fi
((i++))
done
((j++))
done
echo output hi.gif
) | flydraw