Infinity. One central mathematical concept on which many myths have spread, especially in the world outside science. Therefore, I had the idea of writing a series of blog-posts about several aspects of "Infinity".

These posts are not scientific, they are for non-Mathematicians, to demystify the concept of "infinity". But neither is it one of those texts that try to include a lot of "history" and interesting side facts. I just want to give a slight understanding of infinity to non-Mathematicians.

So, in this first post, we shall have a short look at the numbers as such. First, everyone knows the non-negative integers . There are "infinitely many" of them, since every number has a unique successor . This should be intuitive to everybody, and in fact, it is an axiom of arithmetic: Every number has a unique successor. Additionally, we have to postulate that every number except has a predecessor.

Another thing you quickly notice: Take an arbitrary sequence of decreasing non-negative integers (that is, start somewhere, and then "count down", possibly leaving steps out), then this sequence will be of finite length: You will soon or later bump into . A bit more complicated, think of an arbitrary set of non-negative integers. Take, for example, the primes, the odd numbers, the even numbers, the phone numbers of your neighbourhood. You will notice that also every of these sets has a minimal element, even though the set itself may contain infinitely many non-negative integers. That is another axiom of arithmetic: Every non-empty set of non-negative integers has a smallest element.

These two axioms plus the existence of are, in fact, sufficient for elementary arithmetic. A whole lot of theorems can just be implied by these axioms. A simple example: Every number is either of the form or - of course, this is not very profound, it essentially states that every number is odd or even, but we only want to give a simple example. To prove it, assume there was some number which cannot be written in that way, then by our axiom, there exists a minimal such . Since , we know that , and therefore, by axiom, it has a predecessor , and as was the smallest number which can not be written in that form, we know  that there is an such that or . If , then , which we did not allow for . If , then , which is also not allowed. This is a contradiction! So, such a cannot exist: All numbers may be written in that form.


Found at KnowYourMemeNow, of course, there are further objects that are commonly called "numbers". When doing accounting, you are certainly familiar with negative integers. So we get the set of all integers, . They do not share the property that every set of them has a smallest element. There are infinitely many of them into "both sides". So intuitively, there are "more" integers than non-negative integers - of course, the latter is a subset of the first.
But what does it mean for two sets of objects to have the same "number" of elements? Let us first look at the finite case. Let us say you are counting apples. You will take one of them and say "one", then a second one, saying "two", and a third one, saying "three", and so on, until no apple is left that was not counted. Let as assume you counted ten apples. You think you just counted the apples, but what you actually did was giving a one-to-one-mapping between apples and the set . Of course, you probably did not memorize the order you chose the apples - because it does not matter which mapping you chose, the important fact is that there is such a mapping. Such a one-to-one-mapping between two sets is called a bijection. Even in our example, there are many such bijections (calculating the actual number is left as an exercise), and you only chose one by random.

So, for the finite case, we can conclude that two sets have the same number of elements, if there is a bijection between them. For the infinite case, this becomes the definition. Two infinite sets are of equal size, if and only if there is a bijection between them.

Now, let us go back to the integers. We tried to conclude that since the non-negative integers are a subset of the integers, there must be less of them. But on the other hand, define a mapping , that is, is . This is a bijection. So in fact, there are as many non-negative integers, as there are integers at all - even though this might not be intuitive, when looking at the finite case.

In fact, this strange behaviour of infinite sets can be used to classify them: A set is finite if and only if there is no bijection into one of its proper subsets. As there are other (mostly equivalent) definitions of finity and infinity, the concept defined here is sometimes called Dedekind-Finity.


Found at Fukung. This concept is probably hard to understand for a non-Mathematician. The problem is that "finity" is such an intuitive concept, that every non-Mathematician will postulate it was "clear". But this is not the mathematical way of thinking. We will get deeper into this topic in one of the following posts on infinity, when we look at cardinalities. For now, let us get back to numbers.

Of course, even a non-Mathematician knows that there is more than integers. We can extend the numbers to fractions. The set of fractions is called , and it contains all fractions of the form where and are integers, where . Fractions have a nice property: between two distinct fractions, there is always a third one. For example, between and , there is . Even worse, from this directly follows that between two distinct fractions, there are always infinitely many other fractions.

For example, between and , there are the fractions . We have "infinity on finite place", so infinity does not yield distance in any sense. Even worse, we will later show that there is a bijection between integers and fractions: Even though we can squeeze infinitely many of them between and , there are not "more" fractions than integers in the above sense.

As everybody should know from school, every fraction can also be written as a decimal fraction, with either finitely many digits or as a recurring fraction. However, we always find finitely many digits to specify them exactly.

And as many of you will probably know, there are also numbers that do not have this property. For example, , the constant to calculate the area of a circle, has no finite nore a recurring decimal representation, only approximations can be written that way. In general, every infinite sequence of digits which has a dot after finitely many steps can be considered a number, like , , etc., and the set of these numbers are called the real numbers, and their set is called . It can be proved that is actually bigger than . We will later see, how this is done.


Found at Mighty Wombat. Usually, the general education stops at , even though there is a larger set of numbers, the complex numbers, , which many non-Mathematicians do not consider as numbers, because it goes further than what they usually do with numbers. However, it is relevant in science, and mathematically, it is probably more beautiful than . Besides all real numbers, it contains, for example, the imaginary unit , for which we have , it is (one) "square root" of , which we do not have in .


An object which is often associated with is the real line: The real numbers can be considered an infinite line which contains all of them. Then, the following graphic illustrates a bijection between the real numbers between and and all real numbers:



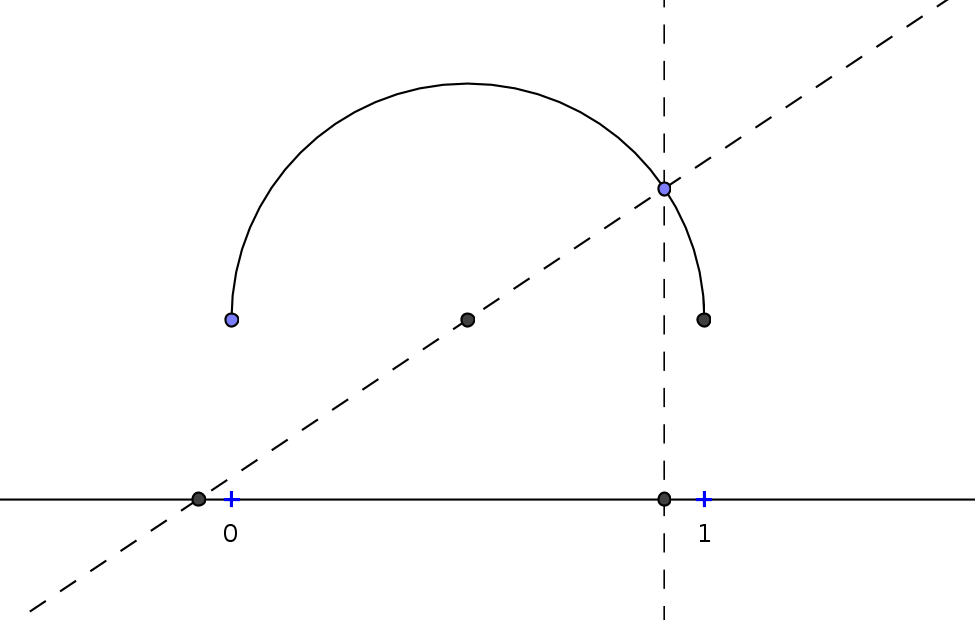
Especially interesting is that and can somehow be considered as the images of the negative and positive "infinity".

So far for this time.

A great article, with interesting references, and as it is about something many people do not seem to understand, worth reading:

> The abstraction-optimization tradeoff

At the station where I leave the train every week, there is a tunnel where often street musicians play their music. Mostly, their play is so bad and annoying that you want to pay them rather for stopping it, than for playing. However, today, I heard some nice melody from this tunnel, and I thought, maybe a band or something is playing there.

Approaching the source, I saw an old woman, playing on a small electrical piano. Looking a little closer, I found that some keys were missing on the keyboard, and obviously, she was only pretending to play - her keystrokes did not sync with the music, the music was obviously played by that gadget automatically.

I am not sure whether this person was snaky, or just naive to think that nobody will notice, or both. However, at least she knew how to play this gadget in a way that it does not make annoying sounds, even though that only means to choose a track and play it, it is better than what the other people do. And that wtf-feel about it somehow made me smile. I gave her 50 cent, to help her repairing the missing keys on her keyboard.

... gab letzens eine Mitarbeiterin der geliebten TU-Mensa von sich, vermutlich unüberlegt und genervt vom Riechverhalten meines Kommilitonen.

Meinen Kommentar, dies sei im Allgemeinen ein schlechtes Motto für eine Küche, hat sie offenbar nicht verstanden.

... you cannot do anything about it. It sometimes happens. And sometimes it comes so fast, that you cannot react properly on it. But mostly, you notice that you have to cough before you do it.

Especially, you can put something in front of your mouth. Even if it appears like nothing leaves your mouth, when coughing, you spit some stuff, even if you do not see it. That is why children are told to put their hands in front of their mouths.

Usually, this is not a good idea, since you will touch a lot of other stuff with your hand. One should better use either some tissue, or your elbow.

However, it appears that many people have not been told to do so. When sitting in trains or busses, especially in winter, I see people szneesing and coughing, without putting something in front of their mouth, almost every time.

This is disgusting! And it is antisocial - it makes other people sick!

Sie ist endlich da ...


... Besser spät als nie!

I already wrote about a campaign "Vergoogeln Sie keine Zeit" (do not waste your time with google) in my university's library. I usually try not to use it, but today, I was looking for a book to learn for my current tests, about algebraic curves.

... an den wichtigen Stellen wird sie nur von Nieten zusammengehalten.

(via)

So, finally, this is part 4 of my series about the irrefutability of the AC from ZF. We are almost there!

Theorem 1: Let ZF-Formulae be given. Then . We then say that reflects the .
Proof: Let be given. Without loss of generality we may assume that the can be written without universal quantifiers, as we can replace every universal quantifier by a negated existential quantifier of the negated quantfied formula.
Recursively define a sequence where and is the smallest ordinal , such that if is a subformula of one of the , we have . Let be the supremum of the . It is sufficient to show that for all subformulae of any we have , which goes by structural induction. If is of the form this is trivial. The step over is clear. We can assume that every occurence of is in the scope of an occurence of , and therefore, instead of having an induction step for , we have an induction step for : , and let . By induction hypothesis, . For the other direction, let , then . By induction hypothesis, we have .
We can do everything we did in Part 1 as well directly in ZF. Alphabets become sets, and formulae become finite sequences. Especially, there is a set of all formulae, which is countable. Notice that there is no need to fix a special "encoding" for formulae, it is clear that one exists, and it is clear that all such encodings have to be equivalent. For a ZF-formula , let be its embedding into ZF, that is, is a set.

For every set we can define an interpretation, interpreting by . We write if this interpretation (for all valuations) models , notice that in this case, is a relation inside ZF. Trivially, we have .

Definition: Now we can define the class of of ordinal definable sets:



where we write to denote that there must exist an encoded ZF-formula.

This class is interesting, as it messes around with the intuition about two meta-layers. However, it is not yet our goal.

Definition: The transitive closure of a set is the smallest such that every element of is also subset of .

Definition: The class of hereditary ordinal definable sets is defined by



Since , trivially .

Lemma 1: .
Proof: "=>": From directly follows , therefore, . For we have , that is, , therefore, .
"<=": For and we have . Therefore, .
Lemma 2: For every ZF-formula we have .
Proof: Let , such that , and . By Theorem 1 there is a such that reflects , therefore .
Theorem 2: is an inner model.
Proof: Due to Part 3, it is sufficient to show (I1), (I2) and (I3). By Lemma 1, (I1) holds.
Let , and such that . Then trivially, . But by Lemma 2 we have . Trivially, we also have , so by Lemma 1, . Thus, (I2) holds.
For (I3), let be a -formula, choose arbitrary , and let . Then by (I1), so by Lemma 1, it is sufficient to show that . As we have , therefore there are and and for there are , sucht hat and . Let , and . By Theorem 1 we get a such that reflects . Therefore





which is in . Therefore, .
Lemma 3: There exists a surjective functor .
Proof: In Part 2 we proved that there is a bijection , so it is sufficient to give a surjective functor . Now let be an enumeration of all ZF-formulae. Define



Then is surjective.
Lemma 4: There exists a surjective functor
Proof: Since , use .
Theorem: (AC) holds in
Proof: By Lemma 4, we have our surjective . For , define . By Lemma 2 we know that for every , , and since , we have . Let be arbitrary but fixed. Then there exists an such that . Now define a well-ordering by



is a well-ordering, and . Thus, in , the well-ordering theorem holds, therefore, AC holds in .

This is part 3 of my posts about the irrefutability of AC in ZF.

We define a hierarchy of sets, the -hierarchy.

• 
• 
• for limes-ordinals

Furthermore, we have for , which can be shown by a trivial inductive argument.

Theorem: We have .
Proof: Assume there was an which is not in for some . Then it cannot be subset of any , since otherwise it would be element of . Therefore it must contain an element which is not in for every as well. That is, every set not being in any of the must contain a set not being in any of the , hence, we would get an infinite -chain, which contradicts (FUN). □

Definition: The relativization of a formula regarding a class is defined inductively over the structure on by:

• 
  
• 
• 
• 
• 

Intuitively, means that holds in . We will later write to denote that holds, defining yet another additional meaning for .

Definition: A class is called inner model of ZF, if it satisfies

• for all we have
• 
• for all axioms of ZF we have

Remark: is an inner model of ZF, since .

Inner models provide a way of getting new models from models of ZF:

Remark: Let be an inner model of ZF, and be a model of ZF with domain and the -relation interpreted by a relation . Let and be an interpretation with domain and -relation . Then .

Therefore, it is sufficient to give an inner model of ZF satisfying AC to show that AC is not refutable: From a model of ZF, we would get a model of ZF satisfying AC. That is what we are going to do. Before we can do this, we have to do some work to give an alternative classification of inner models.

Definition: A formula is called -formula, if every quantifier is bounded, that is, every universal quantifier is of the form , and equivalently, every existential quantifier is of the form . (Recall that our language does not contain existential quantifiers directly, but defines them by universal quantifiers. However, our definition is equivalent to what we would get directly.)

Notice that is a -formula.

We write for , and for . Furthermore, if we want to denote a list of variables, then we use the vector notation , and we will use to denote the universal quantification over all of these variables.

Theorem I: Let be a class. Then the following propositions are equivalent:

• a. is an inner model
• b. satisfies:
• (I1) Every element of is a subset of
• (I2) For every there is an element such that
• (I3) For every -formula we have

To proof Theorem I, some additional work needs to be done. Firstly, we will replace the replacement scheme by two other schemes:

-comprehension: For every -formula we have .

Limitation: For every ZF-formula we have

Theorem: These schemes are derivable from ZF.
Proof: -comprehension follows by general comprehension, which follows by (RPL). For limitation, let , and be given, and . Define a function ; this is well-defined, since such a always exists according to the above theorem. Then the range of is a set of ordinals, and therefore has a supremum . Now set . Then contains an for every , such that .

We now show the converse, these schemes imply replacement.

Lemma: For every ZF-formula , can be shown by -comprehension and limitation, not using full comprehension.
Proof: Recall that for pairs . We show that from follows : , are sets by -comprehension. By limitation, there exists a set such that for all we have an with . That is, contains a superset of for every , that is is a superset of , thus, is a set due to -comprehension.

We now use structural induction on .

If , then is the desired set.

If is of the form , let be given and let , and is a -formula, which means that is a set by -comprehension.

If is of the form , then and these are both sets by induction.

For notice that , therefore it is sufficient to show the induction step for negations. Thus, let . Then which is a set by induction.

For , by limitation we have a set with . By induction hypothesis, , and therefore . Therefore, by -comprehension, , therefore, .
Lemma: For -formulae and classes such that follows .
Proof: By structural induction. For everything except quantors, the relativization can be looped through. For quantors, we may assume that we always have an existential quantifier, since . So let . We may assume that , since otherwise the formula would be equivalent to . Let , then by induction hypothesis , and therefore . For the other direction, assume , that is, there is some such that . Then implies which implies , so by induction hypothesis, , and since we have , therefore .
Corollary: For -formulae and classes in which every element is a subset we have and

Theorem: From -comprehension and limitation follows replacement.
Proof: Let be a functor, and . By limitation we get a with . Then by the above Lemma.

We finally arrive at...

Proof of Theorem I: "a=>b": (I1) by definition. For (I2), consider the -hierarchy inside , that is, define . For we can find an such t hat , and . For (I3), let be a -formula and let . Because of (I1) we have for all according to the above lemma. Therefore, for every , , which is in by comprehension.
"b=>a": Trivially, is transitive, and as every transitive set of ordinals is an ordinal, either or . Assume , then by (I2) we have an such that . But which is in by (I3), so . Contradiction. Therefore, . We show the ZF-axioms. (EXT) and (FUN) hold because of the above Corollary, (NUL) and (INF) hold since .  For (UNI), let , then and therefore every is subset of , therefore and according to (I2) we find a superset . But then, by (I3). Similar for (PAR). For (POW), let . Then by (I2), since , there exists an such that . Then by (I3), .
We have proven that replacement can be replaced by -comprehension and limitation, therefore, we show -comprehension and limitation in . For -comprehension, let be a -formula. We have to show that . But by the above Lemma, this is the same set as , which is in according to (I3). For limitation, consider again a -formula . Then we have to show . Let , then there exists a such that . By (I2) we get a such that , which trivially satisfies the above formula.