Ich weiß überhaupt nicht, wo ich anfangen soll, und wie ich meine Gedanken dazu gliedern soll. Ich fange vielleicht mal beim temporalen Startpunkt an: Ich sah heute, als ich mit der S-Bahn fuhr, das folgende Plakat - es hat leider ein paar schlieren, da ich es durch eine verregnete Scheibe fotografierte:

Eine Googlesuche ergab: Nicht nur mir fiel dieses Plakat auf.

Die GEMA meint, ohne Komponisten können wir nicht mit Gott singen. Als "Beweis" dieser Behauptung führt sie ausgerechnet "Von guten Mächten" an, weil sie wohl weiß, dass dieses Lied vielen Christen gefällt, und gerne gespielt wird. Ich weiß nicht, ob die GEMA für das Spielen dieses Liedes und etwaiger anderer Lieder die ihr gehören in Gottesdiensten Geld bekommt, oder ob gar die Kirchen einen Pauschalvertrag mit der GEMA haben, dieses PDF lässt auf Letzteres schließen, aber ich habe es nicht ganz durchgelesen. Daran ist nichts auszusetzen, die Kirche hat sich an Gesetze zu halten. Was aber Vielen vielleicht garnicht bewusst ist, ist die unmittelbare Konsequenz daraus: die GEMA verdient damit zumindest indirekt an Gottesdiensten. Und an Beerdigungen, Hochzeiten, und und und. Und zumindest wenn man den allgemeinen Berichten glauben schenkt dürfte es auch im Wesentlichen die GEMA sein, und weniger die Komponisten selbst, aber diesen Fakt kann ich nicht nachprüfen.

Die Botschaft ist jedenfalls klar: Ohne die GEMA gäbe es keine Komponisten, und ohne die gäbe es keine Gottesdienste. Billigste Propaganda, die auf die religiösen Gefühle der Bevölkerung abzielen. Ich möchte bewusst auf die schwierige moralische Bewertung des Themenkomplexes Urheberrecht verzichten. Auch Parallelen zum Ablasshandel möchte ich mir jetzt verkneifen. Man kann über Verwertungsgesellschaften denken wie man will, diese Art von Propaganda ist in jedem Falle unterste Schublade. Da sind mir koranverteilende Muslime unbegrenzt lieber, haben sie doch wenigstens die ehrliche Aufforderung "LIES!" - die Aufforderung der GEMA liest sich eher "ZAHL! Gott will es!".

"Musik ist uns was wert", so der Slogan der GEMA. Dazu gehören meinem Eindruck nach vor Allem Abmahnungen und Verwaltungskosten, und Kosten für propagandistische Werbeplakate.

Nun haben es die Kirchen ja wirklich nicht leicht in letzter Zeit. Ist die Piratenpartei (gegen deren Bewegung sich die Werbeaktion der GEMA wohl primär richten dürfte), die momentan am schnellsten wachsende Partei, an der sich schon die etablierten Regierungsparteien die Zähne ausbeißen, doch für eine stärkere Säkularisierung und hat damit erfolg. Und so kann ich mir vorstellen, dass es einige Christen gibt, die mehr oder weniger unreflektiert gegen Selbige sind (Ich bin ja der Meinung, fortschreitende Säkularisierung tut den Kirchen auf lange Sicht hin gut, aber darum soll es mir hier garnicht gehen.)

Trotzdem hoffe ich, dass die Kirchen sich hier nicht instrumentalisieren lassen, und sich öffentlich davon distanzieren.

A strange situation. I am not sad, it is just a strange mood of sentimentality. Here, everything started. And everything ends. This is the third time that I am here since beginning my studies. There was no reason to go there more often.

And now, my time as an undergraduate is over. I should feel more mature now. But with maturity comes realism. And with realism comes pessimism.

I think there is a great confusion on programming paradigms right now. "Functional vs. Imperative" is, for example, a great discussion, with a lot of strange arguments, mixing together completely different opinions, which have nothing to do with each other.

What does, for example, "functional" mean? Matthias Benkard has pointed out that "functional programming is algebraic programming". And here is a nice article on what "object oriented" means.

So at first, one might ask what such systems of paradigms are good for, anyway. It is not immediately clear why it is useful to make these rather coarse distinctions between languages. And it is questionable whether such classifications give any new insights rather than just being pointless technobabble, inventing concepts just for their own sake.

I think they are useful. They can help us to understand similarities between programming languages, and also their differences, which means that it is easier to compare programming languages. For a low-level image encoder, for example, one will probably not choose a functional language, while for a complex tree reduction, one might consider it as it is optimized for this kind of problems, and will bring you to your goal faster.
Also, when trying to combine languages or their features, it can help estimating the compatibility. It is rather hard, though possible, to have a purely functional language without garbage collection, and is probably not worth the effort. On the other hand, formal verification of imperative code always somehow yields a functional embedding, which makes it mostly not worth the effort.
Furthermore, such a classification makes it easier to learn about programming languages, as you can easily see their similarities and do not need to learn things twice.

One should not forget, however, that every such classification should only be considered as a model. It cannot be absolute, it must be rethought regularly, and it cannot be exhaustive, as long as new concepts evolve.

I will try to give a classification that sounds reasonable for me, but I will also give examples of languages that do not fit in there. My goal is not to aggressively fit every language into some category for its own sake, but to try to point out similarities and differences.
Also keep in mind that most languages are mixtures, and the distinctions here should not be seen in a black-white-manner, but rather as extreme points in some continuous space.
And, as one further thing before I start, I would like to point out a fallacy that many people have when such distinctions are made: You will hardly find a language in which you can not, in theory, emulate the behavior of another language. That is simply due to the fact that most languages are turing complete. However, the classifications address the way of programming a language encourages, rather than what is possible to do with it.

So, the first distinction that sounds reasonable to me is between functional, function-oriented and flat programming languages.

Functional languages are those languages which have functions as first-class objects, and encourage their use. They usually have closures, some have continuations, most have optimizations for tail recursion, and code written in these languages usually makes heavy use of recursion, currying and lambda-abstraction. All Lisps I know are, by this definition, functional. All functional languages I know, except NewLisp, have a garbage collector. While C++ meanwhile has lambda-forms, and and Java has interfaces with closures in their methods, both do not encourage this kind of programming, so they are not functional programming languages. Same for python and perl, in which lambda forms are just a feature, not a principle.
Inside functional languages, the availability of ephemeral data structures can cause many problems due to the deep nesting of objects and functions which is often involved. Therefore, side effects are discouraged in most modern functional languages.

Function-oriented languages do have functions, and they are used for code reuse and modularization, and the user is not required to know the actual mechanisms of a function call. Many of them support recursion and a crude form of function variables, for example function pointers in C, but they are usually used for callbacks only. Function-oriented languages are currently the most widely used type. Old BASIC dialetcs are not function-oriented. Though they have GoSub and Return as directives, these are instructions to manipulate the program flow, rather than structuring the code. Same goes for x86 assembly.

Flat languages do not have functions at all. Most assembly languages are flat. Old BASIC dialects are flat. MS-Dos-Batch-Files are flat. In some sense, also Prolog and SQL are flat. Spreadsheets are flat.

The second classification is to distinguish data-oriented and code-oriented programming languages, where data-oriented programming languages can be algebraic or relational, with object-oriented languages as a special case, and code-oriented programming languages can be liquid and solid (I could not come up with a better metaphor, sorry). Though it might seem so, these categories are not mutually exclusive.

Data-oriented languages focus on the data they work with, rather than the code.

Algebraic languages, as a form of data-oriented languages, focus on the structure of the data they work with. They have strong type systems. They usually have algebraic inductive types and some form of polymorphism, which is why they are usually also functional. Code often involves a lot of datatype definitions rather than actual functions, and functions often consist of a few recursion operators for the algebraic types, that is, case distinctions on what the actual structure of a set of data is, and recursive calls basing on them. Data is mostly immutable, ephemeral data is, if available at all, encapsulated in special operators and definitions in all implemented languages I know, with Xanadu being a yet unimplemented but proposed exception. Haskell, Agda and ML are canonical examples.

Relational languages, as a form of data-oriented languages, focus on the relations between the data entities they work with. They usually have some sort of notion for records, unions and references, and their program states can often be visualized by graphs. Algorithms often involve walking through the graph of data entities, to find paths to objects with a certain property. Prolog, Minlog and  SQL are canonical examples.

Object oriented languages are a special form of relational languages, which focus on equivalence relations between objects. Such equivalence relations are often generated through information hiding. Message-passing and proxifying are techniques to add membership of an object to a class. In most languages, like Common Lisp and Java, there is a cycle-free directed graph of classes of objects which by default inherit, but may overload properties of objects of their classes' parents. To prevent problems like the diamond dispatch problem, it is desirable to keep this graph a tree. In many languages like C++ and Python, these classes are connected to their own namespaces. Object oriented languages are probably the most widely used type. An example for a language which does not have a class graph is the prototype-based language JavaScript. Object systems can be put on almost every other paradigm mentioned here.

Code-oriented languages focus on what is actually done rather than the data involved. They often use techniques of other paradigms, but not as a major tool of programming. They usually do not have strong abstraction barriers over the machine they are run on, and focus on efficiency. They tend to make heavy use of local ephemeral data in loops, with Clojure being a modern exception which enforces encapsulating them using tail recursion, and other Lisp dialects mostly providing possibilities to do so. Code-oriented languages usually require familiarity with the concept of a pointer or reference, even though some of them have garbage collection. All Lisp dialects I know are code-oriented, Lisps are the canonical examples of languages being both code-oriented and functional.

Solid code-oriented languages do not provide a natural way of generating efficient code at runtime. Code and data are treated as separate entities. Therefore, the code can be compiled, but no compiler has to be embedded into the binary, and no dependency added to one. C is a canonical example.

Liquid code-oriented languages allow generation of efficient code at runtime from either source code or abstract syntax trees. Therefore, they must either be interpreted themselves, or the compiled binary must contain some form of compiler. Pico Lisp is a canonical example which uses syntax trees. Nearly every scripting language is an example since it has some form of eval-function. SBCL is an example of a compiler.

So, these were my current thoughts. I might change my opinion, and I am interested in other opinions on that topic.

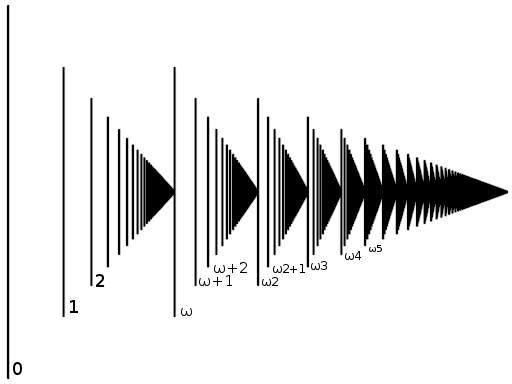
However, there is one sort of ordering relations which especially suits the purpose of describing connections between infinitary objects: the well-orderings. We will introduce this concept here.

In part 1, we gave axioms for natural numbers. These were

Now consider the set of pairs of natural numbers. We give an ordering by

That is, we first sort by the left element, and then, if the left elements are equal, by the right element. This is called the lexicographical order on . It is, in fact, an ordering (exercise).

This relation satisfies our two remaining axioms: The unique successor of a pair is obviously . To get the minimum of a set , we first notice that has a minimal element , as it is a subset of , and  then also has a smallest element , and then, is a minimal element of . The "zero" of this ordering, that is, the smallest element, is obviously .

A further example for a pair with no predecessor is . Even though there are infinitely many pairs, namely smaller than , none of them is the predecessor of .

Now, keep in mind that we still want a generalization of the order of the natural numbers. We can embed into using the injective homomorphism . As mathematicians are lazy, we will now just identify the naturals by this homomorphism, that is, we will actually write instead of . With this inclusion, becomes the first element that is larger than all the "naturals". We will - for now - write for , and for , and - to make it even more confusing - for .

In fact, we can then do addition with these new objects, and multiplication with a new object and a natural, as we did with naturals - with distributive and associative laws:

However, what we cannot do yet is multiplying two of these new objects: is not defined yet. We can generalize the above concept by looking at infinite sequences of natural numbers, which end in a sequence of zeroes, that is, , , etc., and apply the lexicographical order on their reversed sequences:

That is, we get for the largest index such that , and use its order. Our former ordering of pairs can be embedded by .

Now, , and , and generally, , and we can write a sequence as . This definition is only provisional: the actual definition is more complicated, especially, addition is not commutative, . Our definition works well if we always have larger numbers on the left side of the addition, and we will silently ignore the fact that we did not define it for other cases.

Ordering relations like are called well-orderings: A well-ordering on a set is an ordering, for which every subset has a smallest element.

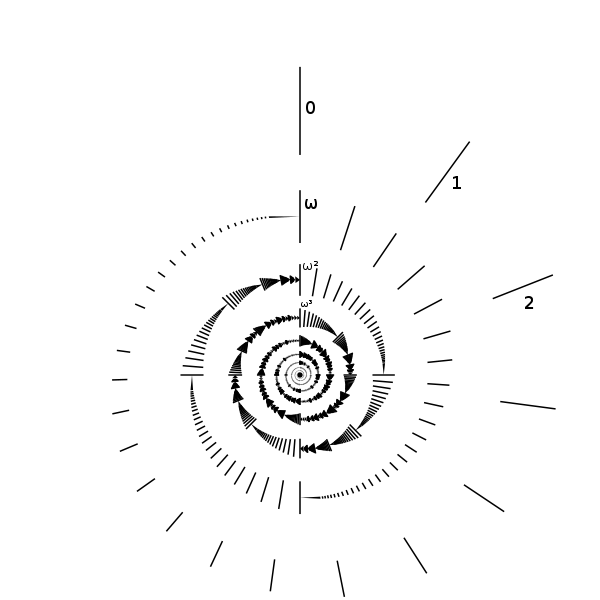
As you have seen in the examples, with well-orderings we can get beyond the tower of natural numbers, into "transfinite" numbers. However, well-orderings have a surprising property, which makes them suitable for analysis of infinity:

Let be a well-ordering, and be a strictly decreasing sequence of elements of . Then is of finite length.

Proof: The set of sequence elements must have a smallest element. As is strictly decreasing, after reaching this element, must end immediately.

Interestingly, we can now find an ordering relation on well-orderings: Let and be well-orderings, then there is either an injective homomorphism or an injective homomorphism or both, when they are isomorphic - as this is a bit harder to prove, we omit the proof.

So we can find a relation between well-orderings, where shall mean that there exisit an injective homomorphism . If we have  and , then the well-ordernigs are isomorphic, we write for that.

The collection contains all the well-orderings isomorphic to a well-ordering , and as it contains all the relevant structural information of the ordering, it is called the ordering type of .

And now ... it gets complicated. We defined as a collection, but not as a set! The axioms of set theory require sets to obey some restrictions - and this collection does not do so. It is a so-called proper class, that is a collection which is too big to be a set. However, it is not necessary to understand the reasons right now, and so I will not give any. The important thing is that being proper classes makes ordering types pretty hard to handle, which is why mathematicians had to invent a different method. For every ordering type, they gave a representative, that is a well-ordering which is isomorphic to the others, but has an additional property that uniquely determines it. These representatives are called ordinal numbers.

While originally I wanted to discuss ordinal numbers in detail with this post, the post turns out to become longer than I expected. I think, for this time, the amount of new knowledge floating through my dear readers' brains is enough.

http://9gag.com/gag/2875781 - I like growing tomatos, as you may remember.

Unicode Character 'PILE OF POO' - what the world needs!

This week's link list:

Promises (via) - a nice minimalistic game about promises and their value.

How Does A Touchscreen-Phone Work

Sony Foam City - a well-known image comes from there.

How To Create An Invisible Folder In Windows - well, sort of, at least.

Artificial Burger Just around the Corner? - Well, probably it will take some more years, but anyway, this kind of research is interesting!

A deep-sea fish with a transparent head and tubular eyes - a weird creature.

Lifter Technology - I wonder whether this effect will be used for something someday.

How to Hack WPA WiFi Passwords by Cracking the WPS PIN

Fish Mimicking Robot - may be used to lead fishes someday.

Oscar The Bionic Cat - There is more interesting stuff about cats than lolcats.

Animated Screenshots

jhead - Exif JPEG Header Manipulation Tool

Coin Game - A coin can be placed anywhere it is touching two other coins.